Понятие определителя вводится только для
матрицы-строки; матрицы-столбца; матрицы размера m×n, где m > n; матрицы размера m×n, где m = n; квадратной матрицы. 12. Укажите верные равенства:
13. Пусть А – квадратная матрица третьего порядка, | А | – ее определитель. Укажите верные равенства:
14. Алгебраическим дополнением Аik элемента aik матрицы А называется число матрица число число число
15. Пусть А – матрица третьего порядка. Укажите, какие из следующих чисел являются членами определителя | А |: a 11 a 22 a 33; a 13 a 22 a 31; a 11 a 12 a 13; – a 11 a 23 a 32; a 21 a 32 a 13.
Вопросы по теме для подготовки к экзамену и контрольному тестированию (ОК-1, ОК-20, ОК-22): Общий базовый уровень: №1. Задан список элементов матриц с указанием их положения в строке и в столбце: a 11=-2, a 22=0, a 33=-1, a 12=2, a 21=-1, a 13=3, a 23=5, a 31=1, a 32=-1. Составьте из этих элементов матрицы A (1x2), A (3x1), A (2x2), A (2x3). № 2. Перемножить матрицы в том порядке, как они записаны и, если возможно, то и в обратном порядке: а) в) д) Уровень углубленного изучения: №2. Матрица A составлена из нескольких подматриц B, C, D, F разных размеров, как указано ниже. Запишите совокупность правил, позволяющих находить элементы матрицы по заданным элементам матриц (подматриц) B, C,D, F и наоборот. A=
Специализированный уровень (ПК-13, ПК-30): №3. Матрица А = №4. Предприятие выпускает продукцию трех видов (столы, стулья и тумбочки) и использует сырье двух типов (сосну и ДВП). Нормы расхода сырья на 1 у.е. продукции заданы матрицей А = Необходимый для повторения теоретический материал по теме: "Решение систем линейных уравнений по формулам Крамера, матричным методом и методом Гаусса"; Обратная матрица. Квадратная матрица, определитель Δ;которой не равен нулю, называется невырожденной, или несобственной, матрицей, а матрица с Δ;=0 называется вырожденной, или особенной, матрицей. Матрица А-1 называется обратной для квадратной матрицы А·n-го порядка, если А· А-1= А-1· А=E. Если определитель Δ; матрицы А не равен нулю, то матрица А-1 существует, причем единственная: А-1 = В сокращенной форме (1): А-1 = Свойства обратной матрицы: 1) (А-1)-1= А; 2) (А·В)-1= В-1 · А-1; 3) (АТ)-1 = (А-1)Т.
|

 ;
;  ;
; ;
;  ;
; .
. ;
;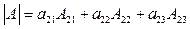 ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; .
.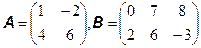 ;б)
;б)  ;
; ; г)
; г)  ;
;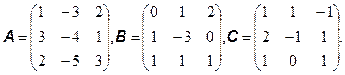
 или
или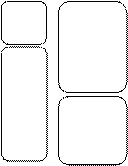 А =
А = 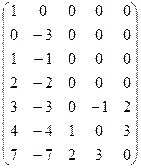
 задает распределение ресурсов трех видов (электроэнергии, трудовых и водных) по двум отраслям экономики (промышленности и сельскому хозяйству) в усл. ед. В этой записи элемент а 11 показывает, что промышленность потребляет 5,3 у.е. электроэнергии. Что в матрице А показывает каждый из элементов: а 12, а 21, а 22, а 31, а 32?
задает распределение ресурсов трех видов (электроэнергии, трудовых и водных) по двум отраслям экономики (промышленности и сельскому хозяйству) в усл. ед. В этой записи элемент а 11 показывает, что промышленность потребляет 5,3 у.е. электроэнергии. Что в матрице А показывает каждый из элементов: а 12, а 21, а 22, а 31, а 32? . Стоимость 1 у.е. сырья каждого типа задана матрицей (ден. ед) В =
. Стоимость 1 у.е. сырья каждого типа задана матрицей (ден. ед) В =  . План выпуска продукции задан матрицей С =
. План выпуска продукции задан матрицей С =  . Определить затраты сырья, необходимые для планового выпуска продукции и общую стоимость сырья.
. Определить затраты сырья, необходимые для планового выпуска продукции и общую стоимость сырья.

 (1), где Аij—алгебраические дополнения элементов матрицы А.
(1), где Аij—алгебраические дополнения элементов матрицы А.


