Определители второго, третьего и высших порядков. Их свойства и методы вычисления. Решение систем линейных уравнений по формулам Крамера, матричным методом и методом Гаусса
1. Исследовать совместность следующих систем. а) в) д)
2. Решить системы уравнений матричным методом: а) в) д)
3. Решить системы уравнений по формулам Крамера: а) в) д)
4. Исследуйте системы и в случае совместности решите их методом Гаусса или Жордана-Гаусса: а) в) д) ж) и) л)
5. Найти фундаментальную систему решений и общее решение следующих систем: а) в) д) Ответы. 1. а) система несовместна; б) система совместна; в) система совместна; г) система несовместна; д) система совместна; е) система совместна. 2. а) 3. а) (16;7); б) (2;-1;1); в) (1;3;5); г) (3;1;-1); д) (-3;2;1); е) (-1;1;-2). 4. а) (с; л) Ø; м) Ø; н) (0; 1; 2); о) ( 5. а) ( д)
ПЛАНЫ Лабораторных занятий по дисциплине «Математика»
Направление подготовки: 36.03.02 "Зоотехния" Профили: "Кормление животных и технология кормов";, "Разведение, генетика и селекция животных";, "Технология производства продукции животноводства";
Факультет: зооинженерный
Форма обучения: очная, заочная
МОДУЛЬ Лабораторное занятие №1 Темы: Матрицы. Основные операции с матрицами. Определители второго, третьего и высших порядков. Их свойства и методы вычисления. Решение систем линейных уравнений по формулам Крамера, матричным методом и методом Гаусса (2 часа) Занятие проводится в интерактивной форме – в форме работы малых групп Учебно-познавательные цели занятия: осмысление и усвоение правил действий над матрицами; научить студентов различным приемам вычисления определителей; ознакомиться с методикой решения систем линейных уравнений, используя методы Крамера, матричный метод и метод Гаусса Воспитательные цели: Развивать алгоритмическую культуру студентов, повышать интерес к предмету в процессе решения задач Развивающаяцель – развитие творческих способностей студентов. На лабораторном занятии формируются понятия: - матрицы (прямоугольной, квадратной, матрицы-строки, матрицы-столбца, диагональной, единичной, обратной и т.д.) - определителя второго, третьего и высших порядков; - решения системы линейных уравнений: - совместной, несовместной, определенной и неопределенной систем; - обратной матрицы; - элементарных преобразований матрицы. На занятии формируются знания: - свойств операций над матрицами; - свойств определителей квадратных матриц; - формул Крамера; - матричного метода решения систем; - метода Гаусса. умения: - выполнять операции над матрицами (складывать, умножать на число, перемножать матрицы; транспонировать); - вычислять определители различными способами; - находить обратную матрицу для данной невырожденной; - решать системы линейных уравнений методом Крамера,матричным методом и методом Гаусса. навыки: - аргументированного письменного изложения собственной точки зрения; - критического восприятия информации компетенции: - ОК-1 – владение культурой мышления, способностью к восприятию, обобщению и анализу информации, постановке цели и выбору путей ее достижения; - ОК-20 – способен к решению нестандартных задач в соответствии с потребностями общества; - ОК-22 – способен к самообучению в течение всей жизни; - ПК-13 - в организационно-управленческой деятельности способностью анализировать и планировать технологические процессы как объекты управления; - ПК-30 - владеет математическими методами анализа и умеет применять их в профессиональной деятельности.
Материально-техническое оборудование: мультимедийный проектор, ноутбук, презентация «Матрицы и определители». ПЛАН ЗАНЯТИЯ 1. Инструктаж по ТБ. 2.Проверка знаний студентов — их теоретической готовности к выполнению заданий по каждой из следующих тем:
|

 б)
б) 
 г)
г) 
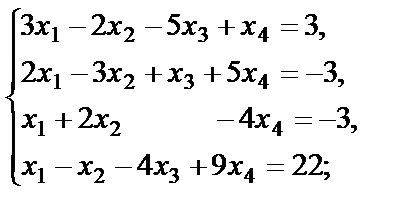 е)
е) 
 б)
б) 
 г)
г) 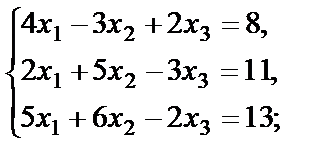
 е)
е) 
 б)
б) 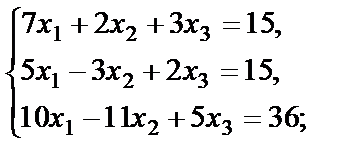
 г)
г) 
 е)
е) 
 б)
б) 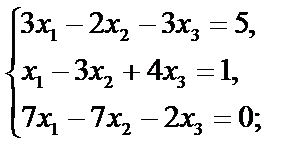
 г)
г) 
 е)
е) 
 з)
з) 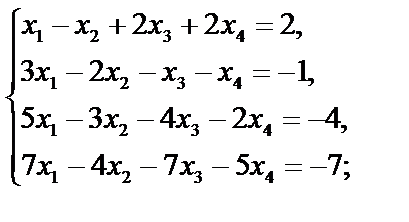
 к)
к) 
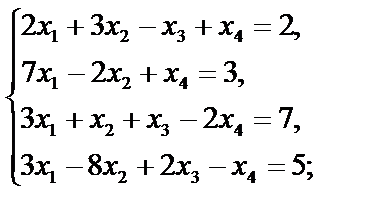 м)
м) 

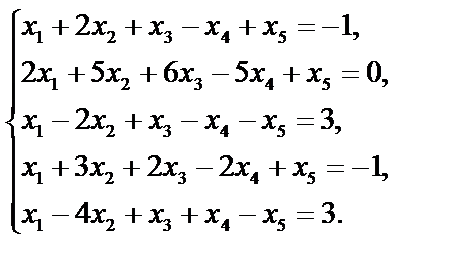
 б)
б) 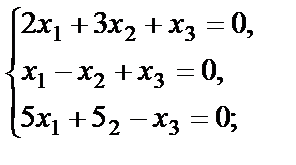
 г)
г) 
 е)
е) 
 ; б) (-3;2;1); в) (3;0;1); г) (3;-2;-5); д) (8;4;2); е) (-8;-4;-13).
; б) (-3;2;1); в) (3;0;1); г) (3;-2;-5); д) (8;4;2); е) (-8;-4;-13). ;
; 
 с); б) Ø; в) (-1;3;2); г) (2;3;1); д) (2;1;3); е)
с); б) Ø; в) (-1;3;2); г) (2;3;1); д) (2;1;3); е)  ; ж) (1; 0; 2); з) (5с-5;7с-7;с;0); и) (
; ж) (1; 0; 2); з) (5с-5;7с-7;с;0); и) ( ); к) (
); к) (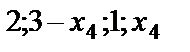 );
);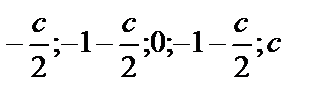 ).
). ); б) (0;0;0); в) (0;0;0); г)
); б) (0;0;0); в) (0;0;0); г)  ;
; ; е)
; е)  .
.


