Решение.
(Для приведения матрицы
Так как число переменных в системе (4) больше числа уравнений (3), то одну переменную, например x 4, объявим свободной, (она может принимать любые значения), а остальные переменные выразим через нее.
Проверка: Ответ: (27- с; -8; -2- с; с), с Î R. Замечание. Количество свободных переменных равно разности числа переменных и числа уравнений в получившейся после элементарных преобразований системе. В некоторых задачах, связанных с системами уравнений, бывает важно знать, имеет ли система решение и если имеет, то сколько. Ответить на этот вопрос, не решая систему, позволяют следующие теоремы. Теорема 1. (Кронекера-Капелли) Система линейных уравнений имеет решение тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы. Теорема 2. Если система имеет решение и ранг матрицы системы равен числу переменных, то это решение единственное, а если ранг меньше числа переменных, то система имеет бесконечное множество решений. Пусть система имеет бесконечное множество решений, т.е. r < n, где r – ранг матрицы, n - количество переменных. Определение. r переменных x 1, x 2,…, xr (r £ n) системы (1) называются базисными, если определитель из коэффициентов при них отличен от нуля. Остальные (n-r) переменные называются свободными. Решение системы, в котором все свободные переменные равны, нулю называется базисным. Замечание. Система имеет конечное число базисных решений, не превосходящих Пример 3. Выяснить имеет ли система решение и если имеет, то сколько, не решая ее: а) Решение. а) Найдем ранги матрицы системы и расширенной матрицы:
б)
Ответ: а) не имеет решений; б) имеет бесконечное множество решений. Пример 4. Найти все базисные решения системы уравнений
Решение. Решим систему методом Гаусса. В результате элементарных преобразований получим систему ступенчатого вида:
Так как число переменных – 4, а число уравнений – 2, то 2 переменные являются свободными, остальные 2 – базисными. Общее число групп переменных (по две), которые можно выбирать в качестве базисных из 4-х переменных равно В качестве базисных можно выбрать любые две переменные, определитель из коэффициентов при которых не равен нулю. Для каждой группы переменных вычислим определители из коэффициентов при них:
Итак, базисными могут быть все пары, кроме (x 2, x 3), так как Найдем 1-е базисное решение, взяв в качестве базисных переменных x 1 и x 2,тогда свободными являются x 3 и x 4. Выразим базисные переменные через свободные переменные:
Теперь присвоим свободным переменным, нулевые значения и найдем базисные переменные.
(7; 5; 0; 0) – 1-е базисное решение. Аналогично найдем остальные базисные решения: (7; 0; -5; 0), (3/4; 0; 0; -5/4), (0; -3/5; 0; -7/5), (0; 0; 3/5; -7/5). Проверка:подставим в систему первое базисное решение.
Остальные решения проверяются аналогично. Ответ: (7; 5; 0; 0), (7; 0; -5; 0), (3/4; 0; 0; -5/4), (0; -3/5; 0; -7/5), (0; 0; 3/5; -7/5). Определение. Система линейных уравнений называется однородной, если все свободные члены уравнений равны нулю. Однородная система линейных уравнений имеет вид:
Такая система всегда имеет решение, по крайней мере, нулевое (x 1= x 2=…= xn =0), которое называют тривиальным. Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ранг матрицы системы меньше числа переменных, причем таких решений бесконечное множество. Замечание. Если в однородной системе число уравнений равно числу переменных, то по теореме Крамера такая система будет иметь ненулевое решение тогда и только тогда когда определитель матрицы системы равен нулю, иначе эта система имеет единственное нулевое решение. Пример 5. Решить однородную систему уравнений: Решение. Вычислим определитель матрицы системы.
Ответ: (0, 0, 0). Обозначим решения системы уравнений (7) a1, a2,…, a i, где Определение. Набор линейно независимых решений a1, a2,…, a k однородной системы линейных уравнений называется фундаментальным набором решений, если каждое решение a системы уравнений является линейной комбинацией решений из этого набора. Теорема. Всякий фундаментальный набор решений состоит из n-r решений, где n - количество переменных, а r - ранг матрицы системы. Замечание. Фундаментальный набор решений не единственен. Каждому набору базисных переменных соответствует свой фундаментальный набор решений. Пример 6. Найти фундаментальный набор решений однородной системы линейных уравнений:
Решение. Решим эту систему методом Гаусса. В результате элементарных преобразований получим систему ступенчатого вида:
Если выбрать в качестве базисных переменные x 1 и x 2 (проверьте, что это можно сделать), то x 3, x 4 будут свободными переменными. Решение системы имеет вид (5 с 1-9 с2; -3 с 1+2 с 2; с 1; с 2), с 1, с 2Î R. Это, так называемое, общее решение системы. Т.к. ранг матрицы системы равен 2, а число переменных – 4, то число решений в фундаментальном наборе равно 4-2=2 (см. Теорему 4.5.).Один из способов нахождения фундаментального набора решений состоит в следующем. Выбираем одну из свободных переменных и полагаем ее равной 1, для остальных свободных переменных берем нулевые значения, и определяем значения базисных переменных. Так мы получаем некоторое частное решение данной системы. Выбирая другую свободную переменную и полагая ее равной 1, а остальные свободные переменные – нулю, получим другое частное решение. Так находим все частные решения, число которых совпадает с числом свободных переменных. Эти частные решения и образуют фундаментальный набор решений. Вычисления оформим в виде таблицы:
Итак, получили фундаментальный набор решений: (5; -3; 1; 0), (-9; 2; 0; 1). Любое решение системы может быть представлено в виде линейной комбинации решений из фундаментального набора, а именно: с 1(5; -3; 1; 0)+ с 2(-9; 2; 0; 1)=(5 с 1-3 с 2; -3 с 1+2 с 2; с 1; с 2), с 1, с 2Î R. Если в качестве базисных переменных выбрать другие, например, x 1 и x 4, то мы получим другой фундаментальный набор решений: (1; -0,6; 0,2; 0), (0; -3,4; 1,8; 1). (Проверьте самостоятельно). Ответ: (5; -3; 1; 0), (-9; 2; 0; 1). Контрольные вопросы (ОК-1, ОК-20, ОК-22): 1. Что такое определитель системы линейных уравнений? 2. Какие системы называются совместными, несовместными, определёнными, неопределёнными, однородными, неоднородными? 3. Что такое решение системы? 4. Приведите формулы Крамера для решения систем линейных уравнений 5. Какие системы могут быть решены по формулам Крамера? 6. Что такое матрица системы линейных уравнений? 7. Как записать систему линейных уравнений в матричной форме? 8. Как найти решение системы линейных уравнений в матричной форме 9. Что такое элементарные преобразования матрицы? 10. В чем заключается метод Гаусса для решения систем линейных уравнений? 11. Как найти определитель матрицы методом Гаусса? 12. Как найти обратную матрицу методом Гаусса? 13. Как найти ранг матрицы методом Гаусса? 14. Как методом Гаусса определить, будет ли система совместной или нет, определённой или нет? 15. Как записать базисное множество решений неопределённой системы? 16. Какие неизвестные называются главными, какие свободными? 17. Какими свойствами обладают решения однородной системы линейных уравнений? Практические задания общие (ОК-1, ОК-20, ОК-22): 1. Решить систему по формулам Крамера 2. Решить методом обратной матрицы систему:
Решение. A = Найдем A -1 A -1= Проверка: Подставим найденные значения переменных в систему:
Ответ: (2; 5; 0). 3. Решить системы уравнений методом обратной матрицы и методом Крамера: а) г) 5. Выяснить, имеет ли система решение и если имеет, то сколько? а) в)
Задания для работы в парах (ОК-1, ОК-20, ОК-22):
№1. Решите системы линейных уравнений, применяя метод Крамера: а) №2. Решить матричное уравнение: а) б) №3. Решите систему линейных уравнений, матричным способом: а) 1. Решите систему линейных уравнений, методом Гаусса: а) в) 2.Выяснить, имеет ли система решение и если имеет, то сколько. а) 3. Подобрать l так, чтобы система имела решение:
4. Найти базисные решения систем уравнений: а) в) 5. Решить однородные системы уравнений. Если система имеет множество решений, то найти фундаментальный набор решений: а) г) Рекомендуемое содержание отчета (для студента). 1. Название лабораторной работы 2. Цель и задачи исследований 3. Электронно-вычислительные средства для расчетов 4. Журнал (тетрадь) исследований (вычислений) с обработкой полученных данных в виде таблиц, графиков (по требованию) 5. Выводы 6. Анализ и защита лабораторной работы производится по результатам представленного студенческой группой отчета (перечень сделанного, рекомендации, ответы на рассмотренные в процессе выполнения контрольные вопросы) Преподаватель оценивает знание каждого студента. Литература
|



 ~
~  ~
~  .
.


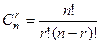 - количество сочетаний из n по r, где n – число переменных, r – ранг матрицы системы.
- количество сочетаний из n по r, где n – число переменных, r – ранг матрицы системы. б)
б) 
 rang A =2, так как
rang A =2, так как  .
. , так как
, так как  . Так как
. Так как  , то по теореме Кронекера-Капелли система не имеет решений.
, то по теореме Кронекера-Капелли система не имеет решений. , rang A =2, так как
, rang A =2, так как  .
. , так как
, так как  . Так как
. Так как  , то система имеет решение. А поскольку число переменных больше ранга матриц, то система имеет бесконечное множество решений (см. Теорему 4.3.).
, то система имеет решение. А поскольку число переменных больше ранга матриц, то система имеет бесконечное множество решений (см. Теорему 4.3.).

 . Это группы (x 1, x 2), (x 1, x 3), (x 1, x 4), (x 2, x 3), (x 2, x 4), (x 3, x 4).
. Это группы (x 1, x 2), (x 1, x 3), (x 1, x 4), (x 2, x 3), (x 2, x 4), (x 3, x 4).





 .
.
 .
.


 . Так как столбец свободных членов уравнений – нулевой, то определители D1, D2, D3, в которых он присутствует, равны 0. Следовательно, по теореме Крамера система имеет единственное решение
. Так как столбец свободных членов уравнений – нулевой, то определители D1, D2, D3, в которых он присутствует, равны 0. Следовательно, по теореме Крамера система имеет единственное решение  .
. некоторое i -е решение.
некоторое i -е решение.



 , B =
, B =  , X =
, X =  .
. . Теперь найдем X: X =
. Теперь найдем X: X = 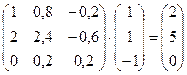 . Итак,
. Итак, 


 б)
б)  в)
в) 
 д)
д) 
 б)
б) 
 г)
г) 
 б)
б)  .
.
 ,
, б)
б) 
 б)
б) 
 г)
г) 
 б)
б)  в)
в)  г)
г) 

 б)
б) 

 б)
б)  в)
в) 




