Метод Гаусса

Метод является универсальным, т.к. он позволяет решать системы линейных алгебраических уравнений с матрицами любой размерности и квадратными матрицами с определителем, равным нулю.

Метод Гаусса состоит в том, что производятся последовательные преобразования исходной системы уравнений в эквивалентную систему до тех пор, пока решение последней не станет очевидным или не станет очевидной неразрешимость системы.

Этот процесс осуществляется с помощью элементарных преобразований система линейных алгебраических уравнений, аналогичных элементарным преобразованиям матрицы до получения матриц эквивалентной системы ступенчатого вида.

Элементарные преобразования системы уравнений:

1.Перестановка любых двух уравнений.

2. Умножение обеих частей уравнения на одно и то же число, не равное нулю.

3. Прибавление к обеим частям одного уравнения системы соответствующих частей другого, умноженных на одно и то же число.

4. Вычеркивание уравнение вида 0·х₁+0·х₂+…+0·х_n=0 как не несущего ни какой информации относительно решений системы.

Пример 1. Решить систему уравнений методом Гаусса

Решение. Выпишем расширенную матрицу системы, состоящую из коэффициентов при неизвестных и свободных членов уравнений (столбец свободных членов отделим вертикальной чертой) и приведем ее к ступенчатому виду.

 

~ ~

Символ «~» между матрицами означает, что матрицы эквивалентны (у них одинаковые ранги), но не равны.

~ = .

Теперь прибавим к 3-й строке 2-ю строку, умноженную 7/5, чтобы обнулить коэффициент при x ₂ в 3-м уравнении.

~ =

Наконец, умножим 3-ю строку на 5, чтобы «избавится» от дробей. В результате преобразований получили матрицу ступенчатого вида.

Эта матрица представляет собой расширенную матрицу системы уравнений, эквивалентной данной системе. Запишем систему уравнений с новыми коэффициентами.

Из последнего уравнения найдем x ₃, из 2-го найдем x ₂, а из 1-го – x ₁.

Проверка:

Ответ: (1; 2; 3).

В этом примере система имеет единственное решение. Рассмотрим пример, когда система имеет множество решений.

Пример 2. Решить систему уравнений:
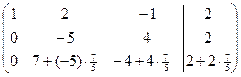