Выучите определения следующих терминов:
матрица, виды матриц, размерность матрицы, сумма двух матриц, свойства операции сложения матриц, умножение матрицы на число, произведение матриц, свойства операции умножения матриц, возведение матрицы в степень, транспонирование матриц, обратная матрица, нахождение обратной матрицы, элементарные преобразования матриц, система линейных уравнений, матричное уравнение, решение матричного уравнения, нахождение решения систем линейных уравнений матричным способом, методом Крамера, решение систем линейных уравнений методом Гаусса.
| № п/п
| Новые понятия
| Содержание
|
|
|
|
|
|
| Матрица
размера 
| это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, образующие матрицу, называются ее элементами.
|
|
| Матрица-строка
| это матрица, состоящая из одной строки;
|
|
| Матрица-столбец
| это матрица, состоящая из одного столбца.
|
|
| Квадратная матрица
n -го порядка
| это матрица, у которой количество строк равно количеству
столбцов и равно n.
|
|
| Диагональная матрица
| это квадратная матрица, у которой все элементы, кроме элементов, стоящих на главной диагонали равны нулю
|
|
| Единичная матрица
| это диагональная матрица, у которой элементы, стоящие на главной диагонали равны единице.
|
|
| Умножение матрицы
на число
| Чтобы умножить матрицу на число  k, необходимо на это число умножить все элементы матрицы k, необходимо на это число умножить все элементы матрицы
|
|
| Сложение матриц
| Чтобы сложить две матрицы одинакового размера, необходимо сложить соответствующие элементы этих матриц
|
|
| Умножение матриц
| а) Две матрицы можно перемножить тогда и только тогда, когда количество столбцов в первом сомножителе равно количеству строк во втором сомножителе.
б) Произведением матрицы 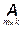 на матрицу на матрицу 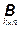 является
матрица является
матрица 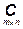 , каждый элемент которой , каждый элемент которой  , стоящий на
пересечении i -й строки и j -го столбца, равен сумме произведений элементов i -й строки матрицы A и j -го столбца матрицы B, т.е. , стоящий на
пересечении i -й строки и j -го столбца, равен сумме произведений элементов i -й строки матрицы A и j -го столбца матрицы B, т.е. 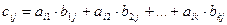 . .
|
|
| Транспонирование матрицы
| Чтобы транспонировать матрицу A необходимо ее строки заменить столбцами с теми же номерами.
|
|
| Определитель квадратной матрицы второго порядкаA = 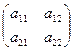
| равен разности произведений элементов главной диагонали и элементов побочной диагонали матрицы, т.е.
D2= 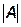 = = 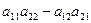 . .
|
|
| Определитель квадратной матрицы третьего порядка A = 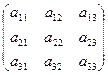
| D3= 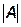 = = 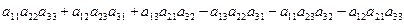 . .
|
| № п/п
| Новые понятия
| Содержание
|
|
|
|
|
|
| Алгебраическим дополнением элемента  квадратной матрицы A n -го порядка квадратной матрицы A n -го порядка
| называется число, которое находят по формуле:
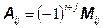 , ,
|
|
| Минором k-го порядка матрицы A размера m х n (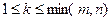 ) )
| называется определитель квадратной матрицы k -го порядка, состоящей из элементов, стоящих на пересечении произвольно выбранных k строк и k столбцов матрицы A.
Обозначение: Mk - минор k -го порядка.
|
|
| Ранг матрицы
| Рангом матрицы называют наивысший порядок отличных от нуля миноров этой матрицы.
Обозначение: rangA или r (A).
|
|
| Обратная матрица для квадратной матрицы А
| Обратной матрицей для квадратной матрицы A называется матрица A -1, такая, что верно равенство:
A×A -1= A -1× A = E.
|
|
| Вырожденная и невырожденная матрицы
| Квадратная матрица называется вырожденной, если ее определитель равен нулю, в противном случае матрица называется невырожденной.
|


 k, необходимо на это число умножить все элементы матрицы
k, необходимо на это число умножить все элементы матрицы
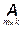 на матрицу
на матрицу 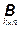 является
матрица
является
матрица 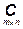 , каждый элемент которой
, каждый элемент которой  , стоящий на
пересечении i -й строки и j -го столбца, равен сумме произведений элементов i -й строки матрицы A и j -го столбца матрицы B, т.е.
, стоящий на
пересечении i -й строки и j -го столбца, равен сумме произведений элементов i -й строки матрицы A и j -го столбца матрицы B, т.е. 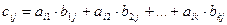 .
.
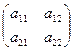
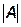 =
= 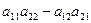 .
.
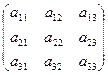
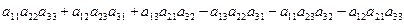 .
.
 квадратной матрицы A n -го порядка
квадратной матрицы A n -го порядка
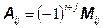 ,
,
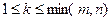 )
)



