План:
I. Полевая трактовка закона Кулона. Напряженность и индукция поля
точечного заряда.
II. 2-я (электростатическая) теорема Остроградского-Гаусса.
III. 4-е уравнение Максвелла как обобщение закона Кулона.
1. Закон Кулона - закон взаимодействия неподвижных точечных зарядов.
Точечный заряд - это абстракция. Точечным зарядом можно считать заряд тела, размерами которого можно пренебречь или, например, размеры взаимодействующих заряженных тел достаточно малы по сравнению с расстоянием между ними.
Рассмотрим два точечных заряда  и
и 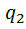 , находящихся на расстоянии
, находящихся на расстоянии  (рис. 3).
(рис. 3).
 рис 3. Два точечных заряда.
рис 3. Два точечных заряда.
Сила, действующая на 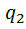 , по закону Кулона равна:
, по закону Кулона равна:
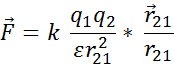
 - коэффициент пропорциональности, зависящий от выбора системы единиц.
- коэффициент пропорциональности, зависящий от выбора системы единиц.
В СИ:  , где
, где  - диэлектрическая проницаемость вакуума.
- диэлектрическая проницаемость вакуума.
В гауссовой системе  . В дальнейшем используется гауссова система единиц – для преемственности с другими разделами теоретической физики.
. В дальнейшем используется гауссова система единиц – для преемственности с другими разделами теоретической физики.
Тогда закон кулона записывается так:
 (1.1)
(1.1)
Формула 1.1 показывает, что может происходить как притяжение, если  и
и 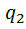 разноименные заряды, так и отталкивание, если
разноименные заряды, так и отталкивание, если  и
и 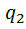 - одноименные.
- одноименные.
Закон Кулона соответствует концепции дальнодействия, так как сила, действующая на 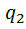 , имеет причину - заряд
, имеет причину - заряд  , находящийся от
, находящийся от 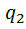 на расстоянии
на расстоянии  .
.
Наша "сверхзадача" - перейти к такой форме, которая связывала бы причину
и следствие в одной точке пространства. Для этого вводим понятие поля.
Сначала определим вектор напряженности поля заряда  в точке 2, где
в точке 2, где
находится заряд 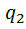 :
:
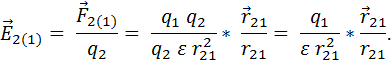
Эта формула не совсем удобна, так как  имеет разное значение в разных средах (зависит от
имеет разное значение в разных средах (зависит от  ). Введем вектор электрической индукции поля
). Введем вектор электрической индукции поля
заряда  , равный:
, равный:
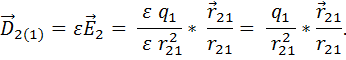
Проведем обобщение этой формулы:
1) сначала отвлечемся от точки 2 и напишем формулу для любой точки поля: 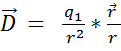 ,
,
2) затем напишем для любого заряда  , создающего поле:
, создающего поле:
 (1.2)
(1.2)
Формула (1.2) означает, что поле вектора  обладает сферической
обладает сферической
симметрией. (Рис.4, а и б).
 а)
а)


б) 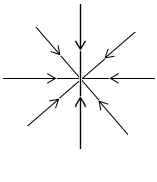
Рис 4. Силовые линии точечного заряда: а) положительный заряд, б) отрицательный заряд.
Это хорошо известные "школьные" картинки. Они показывают, что силовые линии могут выходить (" вытекать") из заряда - случай a), могут входить (" втекать") в заряд - случай б). Что является дифференциальной причиной такого "истока" и "стока" в данной точке поля, нам и предстоит выяснить. Но сначала докажем интегральную теорему для потока вектора электрической индукции, это и есть 2-я (электростатическая) теорема Остроградского-Гаусса.
II. 2-я (электростатическая) теорема Остроградского-Гаусса
Необходимо вычислить поток вектора электрической индукции через
произвольную замкнутую поверхность в случае произвольного распределения заряда, т.е.  . Вычисление проведем в несколько этапов, постепенно обобщая результаты.
. Вычисление проведем в несколько этапов, постепенно обобщая результаты.
I. Сначала вычислим элементарный поток вектора электрической индукции  т.е. поток вектора
т.е. поток вектора  через элементарную площадку
через элементарную площадку  отстоящую от точечного заряда
отстоящую от точечного заряда  на расстоянии
на расстоянии  .
.
Для определенности пусть заряд  - положительный. Тогда (см. рис. 5)
- положительный. Тогда (см. рис. 5)
Рис.5
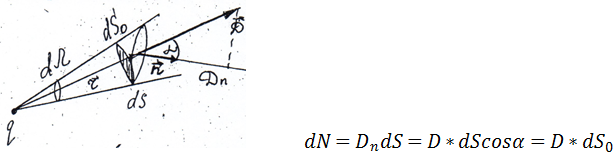
где  - элементарная площадка, перпендикулярная радиусу-вектору
- элементарная площадка, перпендикулярная радиусу-вектору  и равная
и равная  .
.
Подставляем вместо  его значение для точечного заряда, т.е.
его значение для точечного заряда, т.е.  и получаем, что поток равен
и получаем, что поток равен  , где
, где  - элемент телесного угла, под которым из точки, где расположен заряд
- элемент телесного угла, под которым из точки, где расположен заряд  , видны поверхности
, видны поверхности  и
и  . При этом
. При этом  равен
равен
 (1.3).
(1.3).
Обратите внимание на эту формулу. Она показывает, что  может
может
иметь разные знаки, а именно:
 (1.4а)
(1.4а)
 (1.4б)
(1.4б)
Учитывая (1.3) получаем для потока выражение:
 (1.5)
(1.5)
2. Вычислим поток вектора электрической индукции через произвольную
замкнутую поверхность от одного точечного заряда. Для этого используем только что доказанный результат. Рассмотрим два случая:
а) Заряд находится внутри замкнутой поверхности S. Тогда согласно рис. 6:
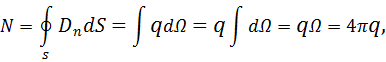
поскольку полный телесный угол, под которым изнутри видна замкнутая поверхность, равен  .
.
 рис 6.
рис 6.
Итак, в этом случае поток равен
 (1.6)
(1.6)
б) Заряд  находится вне замкнутой поверхности S. Тогда поток
находится вне замкнутой поверхности S. Тогда поток
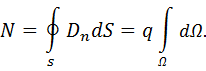
Рассмотрим два элемента поверхности  и
и  , которые из точки, где расположен заряд, видны под одним и тем же по величине телесным углом
, которые из точки, где расположен заряд, видны под одним и тем же по величине телесным углом  (рис.7).
(рис.7).
 рис 7.
рис 7.
Однако площадка  видна под положительным телесным углом
видна под положительным телесным углом  , потому что нормаль
, потому что нормаль  образует острый угол с радиусом-вектором. Площадка
образует острый угол с радиусом-вектором. Площадка  видна под отрицательным телесным углом
видна под отрицательным телесным углом  , так как нормаль
, так как нормаль  образует тупой угол с радиусом-вектором. В сумме же эти два телесных угла компенсируют друг друга, т.е.
образует тупой угол с радиусом-вектором. В сумме же эти два телесных угла компенсируют друг друга, т.е.  . В итоге
. В итоге  . Тогда поток будет равен
. Тогда поток будет равен
 (1.7)
(1.7)
Рассматривая совместно (1.6) и (1.7), запишем:
 (1.8)
(1.8)
Итак, для одного точечного заряда теорема доказана.
3. Пусть имеется система точечных зарядов  . Вычислим
. Вычислим
поток вектора электрической индукции через произвольную замкнутую, поверхность для системы точечных зарядов. Согласно принципу суперпозиции каждый заряд независимо от других создает свою  и соответственно свой поток
и соответственно свой поток  через поверхность
через поверхность  . Но учитывать надо только заряды, находящиеся внутри поверхности
. Но учитывать надо только заряды, находящиеся внутри поверхности  согласно (1.8), так как заряды, находящиеся вне поверхности
согласно (1.8), так как заряды, находящиеся вне поверхности  вклада в поток не дадут. Тогда каждый заряд, находящийся внутри поверхности
вклада в поток не дадут. Тогда каждый заряд, находящийся внутри поверхности  дает поток:
дает поток:
 ,
,  …,
…,
 .
.
Просуммируем эти потоки:
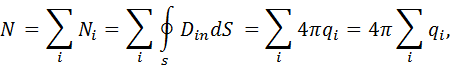
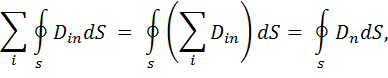
где  и
и  ,
,  .
.
Тогда поток равен:
 (1.9)
(1.9)
Формально получен такой же результат, что и в (1.6), но он применим,
для более общего случая.
4. Рассмотрим непрерывное распределение заряда  по объему V,
по объему V,
ограниченному поверхностью  . Характеристикой такого распределения
. Характеристикой такого распределения
является объемная плотность электрического заряда  , определяемая
, определяемая
следующим образом:
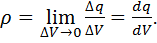 (1.10)
(1.10)
При этом элемент объема  имеет заряд
имеет заряд  , заряд же всего
, заряд же всего
объема вычисляется  , где
, где  в общем случае может зависеть как от координат, так и от времени, т.е.
в общем случае может зависеть как от координат, так и от времени, т.е.  .
.
Разбиваем мысленно объем V на элементарные объемы  такие, что заряд
такие, что заряд  объема
объема  можно было бы считать точечным. Тогда этот заряд равен
можно было бы считать точечным. Тогда этот заряд равен  . Согласно доказанной ранее теореме каждый такой точечный заряд создает свой поток, равный:
. Согласно доказанной ранее теореме каждый такой точечный заряд создает свой поток, равный:
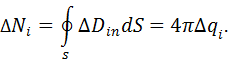
Здесь  - вектор электрической индукции, создаваемой зарядом
- вектор электрической индукции, создаваемой зарядом  . Для этих зарядов так же выполняется принцип суперпозиции. Просуммируем все потоки от зарядов
. Для этих зарядов так же выполняется принцип суперпозиции. Просуммируем все потоки от зарядов  и перейдем к пределу суммы:
и перейдем к пределу суммы:
 (1.11)
(1.11)
Рассмотрим по отдельности каждое выражение, вспоминая, что предел
такой суммы - соответствующий интеграл:
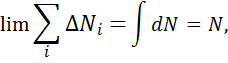
 ,
,
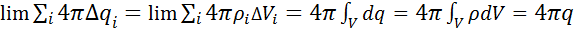 . (1.12)
. (1.12)
Тогда вместо (1.11) на основании равенств (1.12) получаем, что
 (1.13)
(1.13)
Итак, в случае произвольного распределения заряда (см. (1.9), (1.13)) поток вектора электрической индукции через произвольную замкнутую поверхность  равен
равен  , где
, где  - заряд, находящийся внутри поверхности
- заряд, находящийся внутри поверхности  . Если внутри данной поверхности
. Если внутри данной поверхности  нет зарядов, то поток равен нулю. Это и есть 2-я теорема Остроградского-Гаусса. Она позволяет достаточно просто вычислять значение вектора
нет зарядов, то поток равен нулю. Это и есть 2-я теорема Остроградского-Гаусса. Она позволяет достаточно просто вычислять значение вектора  для ряда случаев, т.е. решать конкретные задачи.
для ряда случаев, т.е. решать конкретные задачи.
III. Переходим к нахождению 4-го уравнения Максвелла. Для этого рассмотрим совместно две интегральные теоремы - I-ю и 2-ю теоремы Остроградского-Гаусса. По 1-й теореме (из векторного анализа) запишем для потока любого вектора  :
:
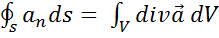 .
.
Для потока вектора  получаем, полагая
получаем, полагая  :
:
 (1.14)
(1.14)
По 2-й теореме для потока вектора 
 .
.
Будем считать, что заряд  распределен по объему с плотностью
распределен по объему с плотностью  .
.
Тогда для потока вектора  можно записать:
можно записать:
 (1.15)
(1.15)
В левой части (1.14) и (1.15) поток вектора  , следовательно, можно
, следовательно, можно
приравнять и правые части:
 .
.
Для элемента объема  получаем:
получаем:
 ,
,  ,
,
откуда следует, что
 (1.16)
(1.16)
Это и есть искомое четвертое уравнение Максвелла.
Выясним его физический смысл. В теоретической физике уравнения записываются следующим образом: в правой части – причина, в левой – следствие. Согласно (1.16) в левой части стоит  . Как известно из векторного анализа дивергенция характеризует источник поля данного вектора. Нас интересует, что является причиной образования источника поля
. Как известно из векторного анализа дивергенция характеризует источник поля данного вектора. Нас интересует, что является причиной образования источника поля  в данной точке. Ответ в правой части уравнения (1.16) - причиной является объемная плотность заряда
в данной точке. Ответ в правой части уравнения (1.16) - причиной является объемная плотность заряда  в этой же самой точке поля.
в этой же самой точке поля.
Итак, причиной источника поля  является объемная плотность заряда
является объемная плотность заряда  в этой же самой точке. При этом возможны три случая:
в этой же самой точке. При этом возможны три случая:
1) если  (положительные заряды), то
(положительные заряды), то  - это означает, что в данной точке "исток"
- это означает, что в данной точке "исток"  ("начало" силовых линий
("начало" силовых линий  );
);
2) если  (отрицательные заряды), то
(отрицательные заряды), то  - это означает "сток" (конец силовых линий
- это означает "сток" (конец силовых линий  );
);

3) если  , то
, то  , но
, но  - это означает, что линии
- это означает, что линии  идут непрерывно:
идут непрерывно:

4-е уравнение Максвелла является обобщением закона Кулона.
1 закон Кулона соответствует концепции дальнодействия, как это уже
отмечалось, потому что причина – заряд  и следствие - сила, действующая на заряд
и следствие - сила, действующая на заряд  , находятся в разных точках пространства.
, находятся в разных точках пространства.
4-е уравнение Максвелла соответствует концепции близкодействия, так как
причина - объемная плотность заряда  и следствие -
и следствие -  связаны
связаны
в одной и той же точке. Таким образом, 4-е уравнение Максвелла описывает любую точку поля, даже такую, в которой отсутствует заряд (см. случай 3).
2 закон Кулона - закон взаимодействия точечных зарядов. 4-е уравнение
Максвелла применимо для любого распределения зарядов и даже тогда, когда  .
.
3 закон Кулона - это закон электростатики. Так взаимодействуют неподвижные заряды.
4-е уравнение Максвелла - уравнение электродинамики. Оно применимо и в
случае  .
.

 и
и 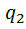 , находящихся на расстоянии
, находящихся на расстоянии  (рис. 3).
(рис. 3). рис 3. Два точечных заряда.
рис 3. Два точечных заряда.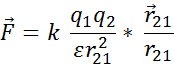
 - коэффициент пропорциональности, зависящий от выбора системы единиц.
- коэффициент пропорциональности, зависящий от выбора системы единиц. , где
, где  - диэлектрическая проницаемость вакуума.
- диэлектрическая проницаемость вакуума. . В дальнейшем используется гауссова система единиц – для преемственности с другими разделами теоретической физики.
. В дальнейшем используется гауссова система единиц – для преемственности с другими разделами теоретической физики. (1.1)
(1.1) .
.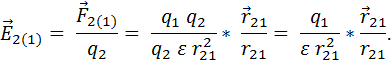
 имеет разное значение в разных средах (зависит от
имеет разное значение в разных средах (зависит от  ). Введем вектор электрической индукции поля
). Введем вектор электрической индукции поля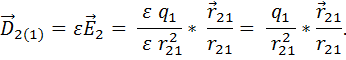
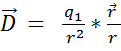 ,
, , создающего поле:
, создающего поле: (1.2)
(1.2) обладает сферической
обладает сферической а)
а)


 . Вычисление проведем в несколько этапов, постепенно обобщая результаты.
. Вычисление проведем в несколько этапов, постепенно обобщая результаты. т.е. поток вектора
т.е. поток вектора  отстоящую от точечного заряда
отстоящую от точечного заряда  на расстоянии
на расстоянии  .
.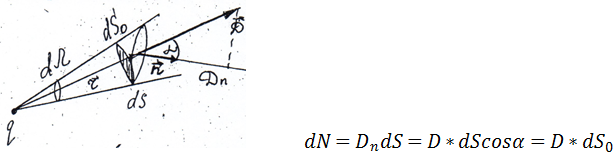
 - элементарная площадка, перпендикулярная радиусу-вектору
- элементарная площадка, перпендикулярная радиусу-вектору  и равная
и равная  .
. его значение для точечного заряда, т.е.
его значение для точечного заряда, т.е.  и получаем, что поток равен
и получаем, что поток равен  , где
, где  - элемент телесного угла, под которым из точки, где расположен заряд
- элемент телесного угла, под которым из точки, где расположен заряд  и
и  . При этом
. При этом  (1.3).
(1.3). (1.4а)
(1.4а) (1.4б)
(1.4б) (1.5)
(1.5)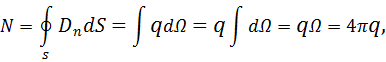
 .
. рис 6.
рис 6. (1.6)
(1.6)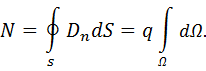
 и
и  , которые из точки, где расположен заряд, видны под одним и тем же по величине телесным углом
, которые из точки, где расположен заряд, видны под одним и тем же по величине телесным углом  рис 7.
рис 7. , потому что нормаль
, потому что нормаль  образует острый угол с радиусом-вектором. Площадка
образует острый угол с радиусом-вектором. Площадка  , так как нормаль
, так как нормаль  образует тупой угол с радиусом-вектором. В сумме же эти два телесных угла компенсируют друг друга, т.е.
образует тупой угол с радиусом-вектором. В сумме же эти два телесных угла компенсируют друг друга, т.е.  . В итоге
. В итоге  . Тогда поток будет равен
. Тогда поток будет равен (1.7)
(1.7) (1.8)
(1.8) . Вычислим
. Вычислим через поверхность
через поверхность  . Но учитывать надо только заряды, находящиеся внутри поверхности
. Но учитывать надо только заряды, находящиеся внутри поверхности  согласно (1.8), так как заряды, находящиеся вне поверхности
согласно (1.8), так как заряды, находящиеся вне поверхности  вклада в поток не дадут. Тогда каждый заряд, находящийся внутри поверхности
вклада в поток не дадут. Тогда каждый заряд, находящийся внутри поверхности  ,
,  …,
…, .
.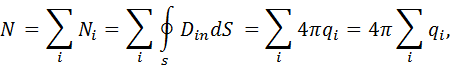
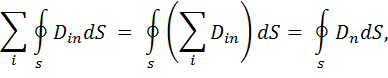
 и
и  ,
,  .
. , определяемая
, определяемая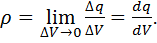 (1.10)
(1.10) имеет заряд
имеет заряд  , заряд же всего
, заряд же всего , где
, где  .
. такие, что заряд
такие, что заряд  объема
объема  . Согласно доказанной ранее теореме каждый такой точечный заряд создает свой поток, равный:
. Согласно доказанной ранее теореме каждый такой точечный заряд создает свой поток, равный: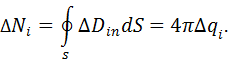
 - вектор электрической индукции, создаваемой зарядом
- вектор электрической индукции, создаваемой зарядом  . Для этих зарядов так же выполняется принцип суперпозиции. Просуммируем все потоки от зарядов
. Для этих зарядов так же выполняется принцип суперпозиции. Просуммируем все потоки от зарядов  (1.11)
(1.11)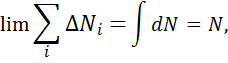
 ,
,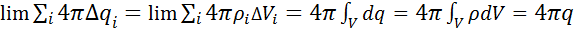 . (1.12)
. (1.12) , где
, где  :
: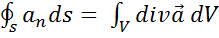 .
. :
: (1.14)
(1.14) .
. (1.15)
(1.15) .
. получаем:
получаем: ,
,  ,
, (1.16)
(1.16) . Как известно из векторного анализа дивергенция характеризует источник поля данного вектора. Нас интересует, что является причиной образования источника поля
. Как известно из векторного анализа дивергенция характеризует источник поля данного вектора. Нас интересует, что является причиной образования источника поля  в данной точке. Ответ в правой части уравнения (1.16) - причиной является объемная плотность заряда
в данной точке. Ответ в правой части уравнения (1.16) - причиной является объемная плотность заряда  (положительные заряды), то
(положительные заряды), то  - это означает, что в данной точке "исток"
- это означает, что в данной точке "исток"  );
);
 (отрицательные заряды), то
(отрицательные заряды), то  - это означает "сток" (конец силовых линий
- это означает "сток" (конец силовых линий 
 , то
, то  , но
, но  - это означает, что линии
- это означает, что линии 
 и следствие - сила, действующая на заряд
и следствие - сила, действующая на заряд  , находятся в разных точках пространства.
, находятся в разных точках пространства. и следствие -
и следствие -  .
. .
.


