Граничные условия для нормальных и касательных составляющих векторов электромагнитного поля
План: I. Необходимость граничных условий. Переходный слой. II. Граничные условия для нормальных составляющих векторов электромагнитного поля. III. Граничные условия для касательных составляющих векторов электромагнитного поля. I. Граничные условия в электродинамике играют двоякую роль: Аналогичная ситуация имеется и в классической механике. Вспомните, например, движение тела под действием силы тяжести. В зависимости от В электродинамике существует проблема - на границе между двумя средами может происходить скачок характеристик среды В электродинамике используются два типа граничных условий - для нормальных составляющих, т.е. для проекций векторов на нормаль к поверхности, и для касательных составляющих, т.е. для проекций на касательное
Рис. 13. Векторы 2 а) Граничные условия для нормальных составляющих вектора электрической индукции. Выберем в переходном слое цилиндр, частично заходящий в первую и вторую среды. Основания цилиндра
Нормали
Интегрируем уравнение по объему цилиндра:
По 1-й теореме Остроградского-Гаусса получаем:
при этом Тогда
Запишем подробно:
Пусть
На боковой поверхности значение
Рассмотрим проекции:
Для
Тогда
подставим в (1.65) и получим:
Теперь переходим к границе, это значит, что
Разделим на
Это и есть искомое граничное условие. Оно означает, что при переходе через границу двух сред нормальная составляющая вектора электрической индукции меняется скачком, если граница заряжена с поверхностной плотностью Если граница не заряжена с поверхностной плотностью, т.е.
Задание №1. Написать граничные условия для нормальных составляющих вектора электрической напряженности, используя условие (1.67), уравнение 2 б) Граничное условие для нормальных составляющих вектора магнитной Для получения этого условия можно использовать рисунок 14. Затем, полагая, что во всех точках поля внутри цилиндра выполняется 3-е уравнение Максвелла
Условие (1.69) означает, что нормальная составляющая вектора магнитной Задание № 2. Написать граничные условия для нормальных составляющих вектора магнитной напряженности, используя условие (1.69), уравнение связи 3 а) Граничные условия для касательных составляющих вектора магнитной Выберем в переходном слое рамку со сторонами
Для любой точки поля внутри рамки записываем 1-е уравнение Максвелла и проектируем его на нормаль
Интегрируем по площади
По теореме Стокса преобразуем:
Затем разбиваем интеграл по замкнутому контуру рамки на интегралы по ее сторонам:
Рассмотрим
при этом учтено, что векторы
Аналогично, учитывая, что
По теореме о среднем преобразуем:
В правой части
где По теореме о среднем преобразуем:
Тогда вместо (1.70) после всех преобразований получаем:
При переходе к границе
Разделим на
Это и есть искомое граничное условие для касательных составляющих (1.71) означает, что если по границе раздела течет поверхностный ток Если по границе раздела поверхностный ток не течет, то скачка нет, касательная составляющая Это всегда имеет место на границе двух диэлектриков, на границе диэлектрик-вакуум. Задание № 3. Написать граничные условия для касательных составляющих 3. б) Граничное условие для касательной составляющей вектора электрической напряженности Используя рис.15 и 2-е уравнение Максвелла
Условие (1.72) означает, что касательная составляющая всегда непрерывна, скачка нет, т.е. Задание № 4. Написать граничные условия для касательных составляющих, Задание № 5. После выполнения заданий 1 - 4 составить таблицу всех
|

 . Это может
. Это может , до
, до  . Проведя необходимые преобразования, для перехода к границе высоту (толщину) переходного слоя устремляют к нулю и получают граничные условия.
. Проведя необходимые преобразования, для перехода к границе высоту (толщину) переходного слоя устремляют к нулю и получают граничные условия. При этом вектор нормали
При этом вектор нормали  направлен в сторону перехода
направлен в сторону перехода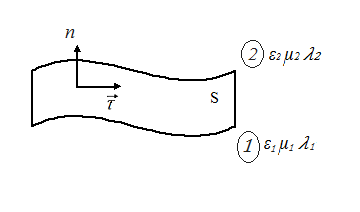
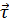 к поверхности раздела
к поверхности раздела и
и  равны
равны  - поверхности на границе
- поверхности на границе  в окрестности точки А. (Рис. 14).
в окрестности точки А. (Рис. 14). Рис. 14 Цилиндр в переходном слое
Рис. 14 Цилиндр в переходном слое и
и  и общая нормаль
и общая нормаль  на границе
на границе 
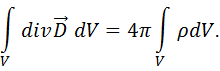

 , где
, где  - заряд, находящийся внутри цилиндра.
- заряд, находящийся внутри цилиндра. (1.65)
(1.65)
 выбраны достаточно малыми, такими, чтобы на каждое из этих поверхностей значение
выбраны достаточно малыми, такими, чтобы на каждое из этих поверхностей значение  было постоянно. Тогда
было постоянно. Тогда
 .
.
 , но поскольку
, но поскольку 
 получаем, учитывая, что
получаем, учитывая, что  .
.
 (1.66)
(1.66) ,
,  ,
,  ,
,  . Тогда получим:
. Тогда получим: .
.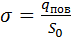 , где
, где  - поверхностная плотность зарядов. Тогда окончательно получим:
- поверхностная плотность зарядов. Тогда окончательно получим: (1.67)
(1.67) и определяется только значением плотности зарядов на поверхности раздела двух сред и не зависит от свойств этих сред.
и определяется только значением плотности зарядов на поверхности раздела двух сред и не зависит от свойств этих сред. , то скачка нет и нормальная составляющая
, то скачка нет и нормальная составляющая  (1.68)
(1.68) и предполагая, что
и предполагая, что  .
.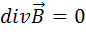 , проводим аналогичные преобразования и получаем:
, проводим аналогичные преобразования и получаем: (1.69)
(1.69) .
. и полагая, что
и полагая, что  .
. , причем
, причем  и
и  равны
равны  , векторы
, векторы  и
и  направлены так, как показано на рис. 15.
направлены так, как показано на рис. 15. Рис.15. Рамка в переходном слое.
Рис.15. Рамка в переходном слое. ,
,
 поверхности рамки и получаем:
поверхности рамки и получаем: (1.70)
(1.70)
 Считая
Считая  ,
, 
 ,
, направлены противоположно. Тогда:
направлены противоположно. Тогда: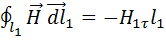 .
.
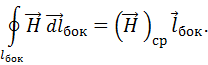
 ,
, – это сила тока, текущего через площадь
– это сила тока, текущего через площадь  .
. .
. ,
,  ,
,  ,
,  , остается:
, остается:
 , где
, где  - линейная плотность поверхностного тока. Окончательно получаем:
- линейная плотность поверхностного тока. Окончательно получаем: (1.71)
(1.71)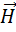 .
. . Величина скачка определяется только значением плотности
. Величина скачка определяется только значением плотности  .
. .
. , используя (1.71) и уравнение связи
, используя (1.71) и уравнение связи  .
. , проводя аналогичные преобразования 3. а), получаем:
, проводя аналогичные преобразования 3. а), получаем: (1.72)
(1.72) .
. и полагая
и полагая  .
. .
.


