Основные свойства поля. Скалярный потенциал, его связь с работой.
Уравнение Основные свойства поля обусловлены его безвихревым характером. Рассмотрим эти свойства. 1) Вычислим работу по перемещению заряда по замкнутому контуру, используя уравнение (2.1) и теорему Стокса:
Итак, работа по замкнутому контуру равна нулю: 2) Покажем, что работа, совершаемая по перемещению заряда между двумя точками поля, не зависит от формы пути. На рисунке 16 это точки Требуется доказать, что работа в этом случае одинакова:
Докажем это свойство, используя только что доказанное №1. Согласно свойству 1 работа по замкнутому контуру
Отсюда
Но работа
т.к. А это работа
следовательно
Рассматривая совместно (2.4) и (2.5) получаем
что и требовалось доказать. Итак, работа, совершаемая по перемещению заряда между двумя точками поля, не зависит от формы пути. Необходимо выяснить, от чего, от какой величины она зависит. 3) Сначала снова используем уравнение
Выберем знак. Для положительного точечного заряда согласно определениям
Поэтому в дальнейшем е электродинамике всегда полагают:
Это основная формула, связывающая вектор 4) Для этого найдем элементарную работу, т.е. работу, совершаемую по перемещению единичного положительного заряда на бесконечно малом пути
при этом использовались выражения для Итак,
Формула (2.7) означает, что в безвихревом поле элементарная работа 5) Найдем, наконец, работу между двумя точками поля, например, точками 1 и 2:
Итак,
Согласно (2.8) работа зависит от разности значений скаляра В некоторых случаях, если в бесконечности Если
Это означает, что потенциал можно определить как работу, совершаемую
§10. Дифференциальные уравнения для потенциала, их общие решения.
Найдем дифференциальные уравнения для потенциала. Для этого запишем
Используем тождество векторного анализа
при этом полагая Тогда
Подставим вместо
Согласно векторному анализу
Тогда
С учетом этих преобразований вместо 4-го уравнения Максвелла получаем уравнение для
Или разделив обе части уравнения на
Это дифференциальное уравнение для Для однородной среды
Это уравнение Пуассона для потенциала Если
Уравнение Лапласа – однородное дифференциальное уравнение 2-го порядка
Постоянную интегрирования
Постоянную Как видно из решений (2.13) и (2.14), разумно потребовать, чтобы в бесконечности
откуда После нормировки общее решение запишется так:
Формально оно совпадает с потенциалом поля точечного заряда, известного Решение уравнения Пуассона найдем не строго, чисто качественно.
Тогда можно применить полученное решение (2.15) для
Потенциал от всех элементов
Итак,
Это и есть искомое решение уравнения Пуассона, строго оно получается в курсе "методы математической физики". Решения (2.15) и (2.16) отличаются при Решение (2.16) не расходится при
Если В электродинамике дискутируется проблема, обусловленная неоднозначностью потенциала, существует две точки зрения: 1) физического смысла не имеет. 2) Автор придерживается второй точки зрения. Отметим, что неоднозначность потенциала не влияет на значение напряженности и работы. В самом деле:
т.к. Аналогично для работы находим:
Напряженность и работа имеют одно вполне определенное значение. К этой проблеме мы будем возвращаться скова в последующих главах. Теперь учтем все возможные случаи распределения заряда и запишем потенциал:
Тогда электрическая напряженность равна:
Это и есть решение 2-й задачи электростатики в общем виде.
§ 11. Разложение потенциала системы зарядов на больших расстояниях,
|

 означает, что электростатическое поле безвихревое, имеет незамкнутые силовые линии, связано с зарядами. Силовые линии начинаются на положительных зарядах и кончаются на отрицательных.
означает, что электростатическое поле безвихревое, имеет незамкнутые силовые линии, связано с зарядами. Силовые линии начинаются на положительных зарядах и кончаются на отрицательных.

 и D. Указаны два разных пути – через точку K и через точку M.
и D. Указаны два разных пути – через точку K и через точку M.
 Рис. 16 Замкнутый путь
Рис. 16 Замкнутый путь Ее можно разбить на работу из точки
Ее можно разбить на работу из точки  в точку
в точку  и из точки
и из точки  в
в 


 (см. рис. 16)
(см. рис. 16)
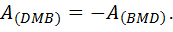

 . Уравнение (2.1) удовлетворяется, как видим,
. Уравнение (2.1) удовлетворяется, как видим,
 и градиента скаляра
и градиента скаляра  имеем в точке М (см. Рис.17)
имеем в точке М (см. Рис.17) Рис. 17
Рис. 17 (2.6)
(2.6) и скаляр
и скаляр  . Необходимо выяснить, что собой представляет введенный таким образом скаляр
. Необходимо выяснить, что собой представляет введенный таким образом скаляр 

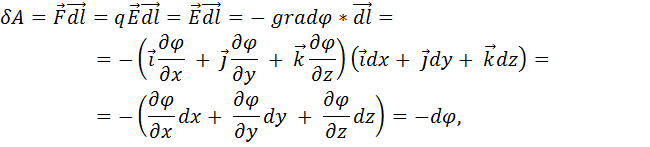
 и
и  в декартовых
в декартовых (2.7)
(2.7)
 (2.8)
(2.8) , можно получить
, можно получить откуда
откуда 
 , то
, то (2.9)
(2.9) . Реально это соответствует случаям,
. Реально это соответствует случаям,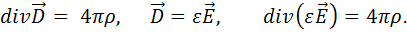








 , получим:
, получим:
 . Тогда вместо уравнения (2.10)
. Тогда вместо уравнения (2.10)

 , то получается уравнение Лапласа:
, то получается уравнение Лапласа:

 можно выбрать в виде
можно выбрать в виде  где
где  – заряд тела (см. Приложение III). Тогда:
– заряд тела (см. Приложение III). Тогда:
 определим из условия нормировки. Нормировка потенциала – процедура придания однозначности потенциалу. Иначе говоря, выбор определенного значения
определим из условия нормировки. Нормировка потенциала – процедура придания однозначности потенциалу. Иначе говоря, выбор определенного значения  . Вполне
. Вполне , то
, то 
 .
.
 , заряженный с объемной плотностью
, заряженный с объемной плотностью  на элементарные объемы
на элементарные объемы  Причем
Причем  имеет заряд
имеет заряд  такой, чтобы его можно было считать точечным.
такой, чтобы его можно было считать точечным. Рис. 18 Объем
Рис. 18 Объем 


 . В самом деле, согласно (2.15)
. В самом деле, согласно (2.15)  при
при  :
:
 не уменьшается с уменьшением
не уменьшается с уменьшением  ,
,






