Е уравнение Максвелла как обобщение закона Био-Савара-Лапласа. Уравнение непрерывности. Ток смешения.
План I. 1-е уравнение Максвелла, как обобщение закона Био-Савара-Лапласа для постоянного тока. II. Уравнение непрерывности - дифференциальная форма закона сохранения электрического заряда. III. Гипотеза Максвелла о токе смещения. 1-е уравнение Максвелла для переменного тока. I. Согласно закону Био-Савара-Лапласа магнитная напряженность бесконечного прямого проводника, по которому течет постоянный ток, равна:
где На рис. 10 изображены силовые линии и вектор
Видно, что вектор
Формула (1.29) показывает, что причина - сила тока Но сначала перейдем к интегральной форме. Для этого умножим (1.29) слева и справа на
или
Покажем, что левая и правая части теперь имеют интегральную форму. Вычислим циркуляцию Выберем
Итак,
Теперь нам надо показать, что
Для случая произвольно ориентированной площадки
Тогда
и сила тока равна:
Подставляем полученные интегральные выражения (1.31) и (1.32) вместо (1.30) и получаем:
Используем теорему Стокса для
Совместное рассмотрение (1.33) и (1.34) позволяет записать:
Для элемента поверхности
Поскольку
Но элемент поверхности
Это искомое 1-е уравнение Максвелла для постоянного тока. Возникает вопрос, применимо ли оно и для описания поля переменного тока? Чтобы ответить на этот вопрос, необходимо ввести некоторый критерий, конечно, в дифференциальной форме, позволяющий отделять случай постоянного тока от случая переменного тока. Для этого сделаем отступление и рассмотрим закон сохранения электрического заряда. II. Пусть в некотором объеме V находится заряд
Других способов изменения заряда нет в природе. Это фундаментальный закон природы. Закон можно записать в интегральной форме:
Рассмотрим три разных случая: 1) Пусть 2) Если 3) Если Теперь переходим к дифференциальной форме закона. Пусть заряд
Находим
При этом сделано предположение, что объем не меняется, а все изменение заряда происходит за счет изменения объемной плотности. С учетом полученного выражения вместо (1.36) запишем:
Применим 1-ю теорему Остроградского-Гаусса к вектору
и подставим правую часть (l.38) в (1.37):
Для элемента объема
Так как
Это и есть искомое дифференциальное уравнение, которое называется уравнением непрерывности. Рассмотрим возможные частные случаи. 1) Если 2) Если 3) Если Случаи 1 и 2 - это случаи переменного тока. При этом
Случай 3 - случай постоянного тока. При этом
Итак, получены критерии, позволяющие отделить случай переменного тока III. Проверим, удовлетворяет ли уравнение (1.35) требованиям уравнениянепрерывности. Для этого образуем дивергенцию от уравнения (1.35):
Согласно тождеству векторного анализа Это означает, что уравнение (1.35) удовлетворяет уравнению непрерывности только для постоянного тока. Для переменного тока, как мы получили ранее, Максвелл разрешил это противоречие следующим образом. Он предположил, что в случае переменного тока в уравнение (1.35) надо к вектору
Выясним, как этот дополнительный вектор устраняет противоречие, т.е. согласует уравнение (1.43) с требованиями уравнения непрерывности (1.41) Для этого снова образуем дивергенцию от обеих частей уравнения (1.43):
Но
Теперь имеются две возможности 1) Если 2) Если Это означает, что противоречие с уравнением непрерывности устраняется. Остается найти явный вид
Выразим
Докажем следующее важное свойство для любого вектора
В самом деле,
Это означает, что операторы
Используя (1.46) для вектора
Максвелл предположил, что искомый вектор
Подставив (1.49) в уравнение (1.43), получаем:
Это и есть искомое 1-е уравнение Максвелла. Физический смысл уравнения (1.50): в природе существуют две причины возбуждения вихря магнитной напряженности - это плотность тока проводимости 1-е уравнение Максвелла есть обобщение закона Био-Савара-Лапласа. 1-е уравнение Максвелла соответствует концепции близкодействия, 2) Закон Био-Савара-Лапласа - закон постоянного тока. 1-е уравнение Максвелла обобщено и на случай переменного тока. 1-е уравнение Максвелла в вакууме (при
Уравнение (1.51) показывает, что вихревое магнитное поле создается переменным электрическим полем. Это свойство самого электромагнитного поля, 1. С введением плотности тока смещения в виде (1.49) в уравнениях электродинамики появляется симметрия, отражающая симметрию свойств поля, что особенно хорошо видно на уравнениях для вакуума:
2. Гипотеза о токе смешения "примирила" систему уравнений Максвелла 3. Гипотеза о токе смещения привела к тому, что, как выяснилось в начале 4. Гипотеза о токе смещения оказалась очень плодотворной. Например, она Необходимо отметить, что плотность тока проводимости § 5. Система уравнений Максвелла Запишем систему уравнений Максвелла для среды, причем в левом столбце в СИ, в правом - в гауссовой системе единиц:
Запись уравнений в разных системах единиц, как это и должно быть, не Отметим формальные свойства уравнений: 1) Система уравнений Максвелла - это система дифференциальных уравнений первого порядка в частных производных, что соответствует концепции 2) Уравнения Максвелла – линейные, что соответствует принципу суперпозиции. 3) Уравнения Максвелла симметричны, что отражает свойства поля, и асимметричны, что отражает свойства вещества. 4) Уравнений Максвелла в данной форме четыре. Как известно из векторного § 6. Закон сохранения и превращения энергии электромагнитного поля. Теорема Умова-Пойнтинга. В 1874 г. русский физик Умов защитил докторскую диссертацию на тему: В дифференциальной форме уравнение Умова имеет вид:
Где В интегральной форме теорема Умова может быть записана в вид:
Уравнение (1.52) означает, что изменение данного вида энергии Докажем теорему Умова для электромагнитного поля и выясним вид
Перейдем теперь к доказательству теоремы для электромагнитного поля. Пусть в объеме V, содержащем поле и вещество, под действием поля выделилось некоторое количество тепла
где Наша "сверхзадача" - преобразовать (1.54) так, чтобы можно было сравнить с (1.53). Рассмотрим по этапам эти преобразования 1) Выразим
2) Подставим (1.55) в (1.54), сразу разбивая на два интеграла:
3) Используем тождество векторного анализа: Пусть
Отсюда
Заменим
Это, как видно, преобразование для подинтегрального выражения в первом интеграле (1.56). 4) Подставим (1.57) в (1.56), сразу объединяя похожие члены с
5) В первом интеграле (1.58):
Докажем это. Рассмотрим правую часть и покажем, что получится левая:
где использованы 6) Подставим (1.59) в первый интеграл (1.58) и получим:
7) Преобразуем снова первый интеграл. Считая объем V фиксированным, выносим
8) Преобразуем второй интеграл, используя 1-ю теорему Остроградского-Гаусса:
9) Подставим эти преобразованные интегралы в (1.60) и получим окончательно
Сравниваем (1.61) с (1.53) и даем интерпретацию
где формула (1.62) - формула для энергии электромагнитного поля, Подведем итоги: 1. Доказана теорема Умова-Пойнтинга, т.е. выполнение закона сохранения 2. Получены в явном виде формулы для энергии и вектора плотности потока Обсудим подробнее эти формулы. 1) Энергия электромагнитного поля:
Эта формула означает, что энергия поля распределена (иногда говорят
Объемная плотность электромагнитной энергии
Например, для двух полей плотность энергии
Покажем это. Пусть в некоторой точке согласно принципу суперпозиции Найдем
Тогда где
Это же свойство имеется и для магнитной энергии. 2) Вектор плотности потока электромагнитной энергии - вектор Умова- П. Л. Капица в статье "Энергия и физика" (см. книгу "Эксперимент, теория, практика") отмечал большое значение теоремы Умова-Пойнтинга в связи с предлагаемыми проектами получения электромагнитной энергии. Незнание теоремы Умова-Пойнтинга превращало некоторые предлагаемые проекты в "прожекты", технически неосуществимые в масштабах страны.
|

 ,
,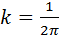 - в СИ,
- в СИ,  - в гауссовой системе.
- в гауссовой системе.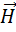 в некоторых точках.
в некоторых точках. Рис. 10. Циркуляция
Рис. 10. Циркуляция  в гауссовой системе единиц:
в гауссовой системе единиц: (1.29)
(1.29) и следствие - магнитная напряженность
и следствие - магнитная напряженность  (радиус силовой линии), что соответствует концепции дальнодействия. Необходимо написать такое уравнение, в котором причина и следствие находились бы в одной точке.
(радиус силовой линии), что соответствует концепции дальнодействия. Необходимо написать такое уравнение, в котором причина и следствие находились бы в одной точке. - длину окружности, т.е. длину силовой линии радиуса
- длину окружности, т.е. длину силовой линии радиуса 
 (1.30)
(1.30)
 , совпадающим по направлению с
, совпадающим по направлению с 
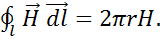 (1.31)
(1.31)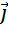 .
.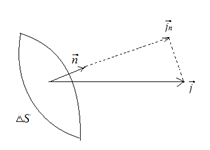 Рис. 11. Вектор
Рис. 11. Вектор 
 проводника, через которую протекает ток
проводника, через которую протекает ток  , получаем:
, получаем:

 (1.32)
(1.32) (1.33)
(1.33) (1.34)
(1.34)
 , следовательно, выполняете равенство:
, следовательно, выполняете равенство:
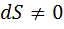 , то можно написать:
, то можно написать: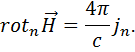
 (1.35)
(1.35) . За счет чего может происходить изменение заряда
. За счет чего может происходить изменение заряда  , ограничивающую объем V (см. Рис.12), т.е. за счет силы тока
, ограничивающую объем V (см. Рис.12), т.е. за счет силы тока  Рис. 12. Заряд в объеме V.
Рис. 12. Заряд в объеме V. (1.36)
(1.36)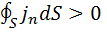 - это означает, что заряды вытекают из объема V. Согласно (1.36)
- это означает, что заряды вытекают из объема V. Согласно (1.36)  , т.е. заряд
, т.е. заряд  , т.е. заряды втекают в объем V через поверхность
, т.е. заряды втекают в объем V через поверхность  Это значит, что заряд увеличивается.
Это значит, что заряд увеличивается. , то и
, то и  - заряд сохранится. Значит в исходном уравнении (1.36) знаки выбраны правильно.
- заряд сохранится. Значит в исходном уравнении (1.36) знаки выбраны правильно. . Тогда заряд представим так:
. Тогда заряд представим так:

 (1.37)
(1.37) (1.38)
(1.38) (1.39)
(1.39) справедливо равенство:
справедливо равенство:
 , то получаем:
, то получаем: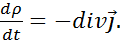 (1.40)
(1.40) , то
, то  – т.е. плотность заряда
– т.е. плотность заряда  , то
, то  - т.е. плотность заряда в данной точке увеличивается, если ток втекает.
- т.е. плотность заряда в данной точке увеличивается, если ток втекает. при
при  , то
, то  и
и  – ток течет, но плотность заряда
– ток течет, но плотность заряда  не меняется.
не меняется. (1.41)
(1.41) (1.42)
(1.42)
 получаем, что
получаем, что и, следовательно,
и, следовательно,  , но уравнение (1.35) этого не дает. Возникает противоречие между фундаментальным законом (уравнение непрерывности) и частным уравнением (1.35).
, но уравнение (1.35) этого не дает. Возникает противоречие между фундаментальным законом (уравнение непрерывности) и частным уравнением (1.35). добавить еще некоторый вектор, который он назвал вектором плотности тока смещения, т.е.
добавить еще некоторый вектор, который он назвал вектором плотности тока смещения, т.е.  . Иначе, вместо (1.35) надо записать:
. Иначе, вместо (1.35) надо записать: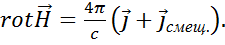 (1.43)
(1.43) .
. ,
,  . Иначе:
. Иначе: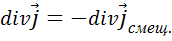 (1.44)
(1.44) , то
, то  - удовлетворяется случай постоянного тока.
- удовлетворяется случай постоянного тока. , то
, то  . Для этого используем уравнение непрерывности (1.40) и соотношение (1.44). Тогда получаем:
. Для этого используем уравнение непрерывности (1.40) и соотношение (1.44). Тогда получаем:
 и подставим в предыдущую формулу:
и подставим в предыдущую формулу: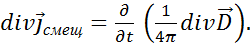 (1. 45)
(1. 45) :
:

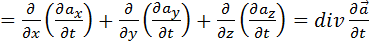 .
. и
и  коммутируют, т.е. их можно переставлять. Аналогично доказывается, что
коммутируют, т.е. их можно переставлять. Аналогично доказывается, что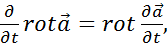 (1.46)
(1.46) (1.47)
(1.47) , можно (1.45) переписать так:
, можно (1.45) переписать так: .
.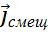 равен:
равен: (1.49)
(1.49) (1.50)
(1.50) и плотность тока смещения
и плотность тока смещения  в данной точке поля. Иначе - магнитное вихревое поле в данной точке создается плотностью тока проводимости и скоростью изменения вектора электрической индукции. Магнитное поле вихревое, имеет замкнутые силовые линии.
в данной точке поля. Иначе - магнитное вихревое поле в данной точке создается плотностью тока проводимости и скоростью изменения вектора электрической индукции. Магнитное поле вихревое, имеет замкнутые силовые линии.
 никакую
никакую  ,
,  ) имеет вид:
) имеет вид: (1.51)
(1.51)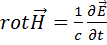 - теоретическое предсказание Максвелла,
- теоретическое предсказание Максвелла,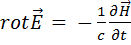 - открытое Фарадеем явление электромагнитной индукции и его обобщение Максвеллом.
- открытое Фарадеем явление электромагнитной индукции и его обобщение Максвеллом. имеют различную природу, но вызывают одинаковое магнитное действие - вихрь магнитной напряженности -
имеют различную природу, но вызывают одинаковое магнитное действие - вихрь магнитной напряженности - 


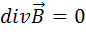
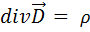
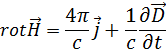







 ) называются уравнениями связи и имеют некоторые ограничения, которые мы рассмотрим подробно в Главе V I.
) называются уравнениями связи и имеют некоторые ограничения, которые мы рассмотрим подробно в Главе V I. и
и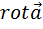 . Но поскольку поле - электромагнитное, то в уравнении поля должно быть две дивергенции (
. Но поскольку поле - электромагнитное, то в уравнении поля должно быть две дивергенции ( и
и  ) и два ротоpa (
) и два ротоpa ( и
и  ). Для описания поля к системе уравнений Максвелла необходимо добавить три основных закона сохранения (см.§ 4) и граничные условия.
). Для описания поля к системе уравнений Максвелла необходимо добавить три основных закона сохранения (см.§ 4) и граничные условия. - сравните с уравнением непрерывности!
- сравните с уравнением непрерывности! - объемная плотность данного вида энергии,
- объемная плотность данного вида энергии,  - вектор Умова - вектор плотности потока этой энергии.
- вектор Умова - вектор плотности потока этой энергии. (1.52)
(1.52) в объеме V может происходить за счет превращения в другой вид энергии с выделением
в объеме V может происходить за счет превращения в другой вид энергии с выделением и за счет втекания или вытекания, т.е. потока данного вида
и за счет втекания или вытекания, т.е. потока данного вида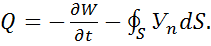 (1.53)
(1.53) (1.54)
(1.54) - дифференциальная форма закона Джоуля-Ленца, известная из курса общей физики.
- дифференциальная форма закона Джоуля-Ленца, известная из курса общей физики. (1.55)
(1.55) (1.56)
(1.56)
 , тогда:
, тогда: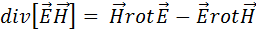 .
. .
. и получим
и получим (1.57)
(1.57) и
и  в один интеграл:
в один интеграл: (1.58)
(1.58) (1.59)
(1.59)

 (1.60)
(1.60)

 (1.61)
(1.61) (1.62)
(1.62) (1.63)
(1.63) .
.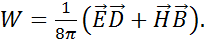 (1.64)
(1.64) , но всегда энергия
, но всегда энергия - положительна. При этом энергия поля и плотность энергии разделяется на электрическую
- положительна. При этом энергия поля и плотность энергии разделяется на электрическую  и магнитную
и магнитную  . Энергия не аддитивна, так как есть еще энергия взаимодействия.
. Энергия не аддитивна, так как есть еще энергия взаимодействия. .
.

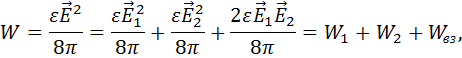
 - энергия взаимодействия, причем энергия взаимодействия может быть положительна, отрицательна или равна нулю, но не превышает энергии поля. Покажем это. Рассмотрим
- энергия взаимодействия, причем энергия взаимодействия может быть положительна, отрицательна или равна нулю, но не превышает энергии поля. Покажем это. Рассмотрим  или
или  или
или 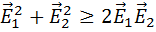 , что соответствует
, что соответствует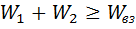 .
. означает, что энергия электромагнитного поля распространяется в пространстве. Материальным носителем энергии является электромагнитное поле. Вся жизнь на Земле обязана энергии Солнца, а доставляется она на Землю электромагнитными волнами!
означает, что энергия электромагнитного поля распространяется в пространстве. Материальным носителем энергии является электромагнитное поле. Вся жизнь на Земле обязана энергии Солнца, а доставляется она на Землю электромагнитными волнами!


