E уравнение Максвелла как обобщение закона электромагнитной индукции
Явление электромагнитной индукции было открыто Фарадеем в 1832 году.
Рис. 8. Поток вектора
Закон электромагнитной индукции с учетом правила Ленца имеет вид:
где При этом эдс индукции возникает (наводится) в контуре Закон (1.20) имеет интегральную форму, что мы сейчас и покажем, а Рассмотрим левую часть (1.20). По определению эдс - это работа, совершаемая по перемещению единичного положительного заряда вдоль замкнутого контура
Итак, получили, что:
Теперь переходим к правой части (1.20). Используем определение магнитного потока:
находим
При этом, считая поверхность фиксированной, предполагаем, что изменение магнитного потока происходит за счет изменения магнитной индукции
Подставляем найденные выражения в (1.20)
Используем теорему Стокса:
Применяем теорему Стокса, полагая
Рассматривая совместно (1.23) и (1.24), получаем:
Для элемента поверхности
Но так как
Мы получили пока соотношение для проекции на нормаль некоторых векторов. Но поскольку элемент поверхности выбран произвольно, нормаль
Это и есть искомое 2-е уравнение Максвелла. Физический смысл 2-го уравнения Максвелла: вихрь электрической напряженности в некоторой точке создается изменением вектора магнитной индукции в той же самой точке. Иначе говоря, переменным магнитным полем порождается вихревое электрическое поле. Вихревое поле имеет замкнутые силовые линии. Если в какой-то точке 2-е уравнение Максвелла показывает, что Фарадей открыл новое по качеству электрическое поле - вихревое, и новый способ создания электрического Но как будет показано в главе II, электрическое поле может быть и безвихревым, т.е. 2-е уравнение Максвелла является обобщением закона электромагнитной индукции: 1) Закон электромагнитной индукции соответствует концепции дальнодействия. В самом деле, как, мы уже отмечали, изменение магнитного поля может происходить в какой-то одной части поверхности S, а 2-е уравнение Максвелла соответствует концепции близкодействия, так 2) Максвелл раскрыл сущность явления электромагнитной индукции - возникновение вихревого электрического поля при изменении магнитного поля, 3) Проводящий контур играет второстепенную роль - роль индикатора, позволяющего обнаружить явление. Но само явление может происходить и без 4) Роль вещества, отметим снова, второстепенная. Запишем уравнение для вакуума. В вакууме
но в среде
Для ферромагнетиков Вообще значение открытия Фарадеем явления электромагнитной индукции и выяснения Максвеллом сущности явления для современное цивилизации огромно и его трудно переоценить!
|

 , опирающуюся на замкнутый проводящий контур
, опирающуюся на замкнутый проводящий контур  , в контуре возникает индукционный ток. (Рис. 8)
, в контуре возникает индукционный ток. (Рис. 8)
 через поверхность
через поверхность  (1.20)
(1.20) - эдс индукции,
- эдс индукции,  - магнитный поток,
- магнитный поток,  - электродинамическая
- электродинамическая , и необязательно через всю поверхность. Может, как показывают многочисленные эксперименты, даже через некоторые участки поверхности. Впечатляющие опыты, в которых участвуют простые школьные приборы (демонстрационный гальванометр, катушка индуктивности и постоянный магнит) сейчас доступны для наблюдения явления на уроках в школе.
, и необязательно через всю поверхность. Может, как показывают многочисленные эксперименты, даже через некоторые участки поверхности. Впечатляющие опыты, в которых участвуют простые школьные приборы (демонстрационный гальванометр, катушка индуктивности и постоянный магнит) сейчас доступны для наблюдения явления на уроках в школе. . Тогда можно записать:
. Тогда можно записать:
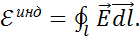 (1.21)
(1.21)
 .
. можно внести под знак интеграла. Итак, получаем:
можно внести под знак интеграла. Итак, получаем: (1.22)
(1.22) (1.23)
(1.23)
 , Тогда:
, Тогда: (1.24)
(1.24)
 выполняется равенство:
выполняется равенство:
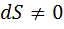 , то
, то (1.25)
(1.25) ориентировано в пространстве соответственно произвольно (см. рис.8), то из равенства нормальных составляющих векторов следует равенство векторов:
ориентировано в пространстве соответственно произвольно (см. рис.8), то из равенства нормальных составляющих векторов следует равенство векторов: (1.26)
(1.26) и направлено вверх (см. рис 9), то
и направлено вверх (см. рис 9), то  направлен вниз. В окрестности этой точки происходит циркуляция вектора
направлен вниз. В окрестности этой точки происходит циркуляция вектора  Рис 9. Связь
Рис 9. Связь  и
и  . Силовые линии такого поля незамкнуты, связаны с электрическими зарядами.
. Силовые линии такого поля незамкнуты, связаны с электрическими зарядами. тогда
тогда  и уравнение имеет вид:
и уравнение имеет вид: (1.27)
(1.27) , тогда уравнение примет вид:
, тогда уравнение примет вид: (1.28)
(1.28) , следовательно ферромагнитные материалы усиливают явление. Это широко применяется в технике.
, следовательно ферромагнитные материалы усиливают явление. Это широко применяется в технике.


