Электрические заряды
Электродинамика изучает макроскопические заряженные тела. Минимальный заряд, существующий в природе в свободном состоянии, равен величине заряда электрона. Заряд реально заряженного тела кратен заряду электрона, поэтому суммарный заряд тела
где qi – элементарный заряд, входящий в состав тела. Для описания заряда и его пространственного распределения введем соответствующие характеристики.
Под точечным зарядом понимают заряд тела, размеры которого много меньше расстояния, на котором оно рассматривается в выбранной системе координат. Если заряд распределен по объему тела, то вводят понятие объемной плотности заряда. Объемная плотность заряда – это заряд, содержащийся в единице объема. Обозначается объемная плотность заряда rе и определяется формулой
Объемную плотность заряда измеряют в кулонах на кубический метр ( Очевидно, заряд элементарного объема определяется формулой
Полный заряд тела, имеющего объем V, равен сумме элементарных зарядов и определяется по формуле
где qT – полный заряд тела, rе – объемная плотность заряда, dV – элементарный объем. В ряде случаев заряд распределен по поверхности тела, поэтому удобно пользоваться поверхностной плотностью заряда s. Поверхностная плотность заряда – это заряд, приходящийся на единичную площадь заряженного тела. Поверхностная плотность заряда
где Dq – заряд, DS – площадь поверхности. Единицей измерения поверхностной плотности заряда является кулон на квадратный метр ( Очевидно, заряд элементарной поверхности находится из выражения
Полный заряд, находящийся на поверхности тела площадью S, определяется формулой
В случае расположения заряда вдоль нити вводят линейную плотность заряда. При идеализированном распределении заряда толщина нити считается нулевой. Линейная плотность заряда – это заряд, приходящийся на единицу длины заряженной нити. Линейная плотность заряда определяется формулой
где Dq – заряд, Dl – длина элемента нити. Единицей измерения линейной плотности заряда является кулон на метр ( Исходя из данного определения, заряд элемента длины нити определяется выражением
Полный заряд, приходящийся на нить длиной L, определяется формулой
Отметим, в реальных условиях распределение заряда является объемным.
где Понятия точечного заряда, поверхностной и линейной плотности заряда являются идеальными, использование которых существенно помогает упростить изучение содержания электродинамики.
|

 определяется формулой
определяется формулой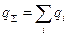 , (1.1)
, (1.1)

 Характеристики
Характеристики
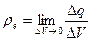 . (1.2)
. (1.2) ).
). . (1.3)
. (1.3) , (1.4)
, (1.4) определяется формулой
определяется формулой
 , (1.5)
, (1.5) ).
). . (1.6)
. (1.6)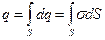 . (1.7)
. (1.7)
 , (1.8)
, (1.8) ).
). . (1.9)
. (1.9) . (1.10)
. (1.10) , (1.11)
, (1.11)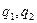 – значения зарядов, r – расстояние между зарядами,
– значения зарядов, r – расстояние между зарядами,  – единичный радиус-вектор.
– единичный радиус-вектор.


