Закон электромагнитной индукции
В истории человечества открытие закона электромагнитной индукции сыграло важную роль, так как именно этот закон дал толчок развитию всей электротехники, позволил создать способы получения электромагнитной энергии, разработать различные типы двигателей и многочисленных устройств. В основе всей электротехники лежит открытие М. Фарадея, который в 1831 году обнаружил появление электрического тока в замкнутом контуре, находящемся в изменяющемся магнитном потоке. В чем заключается сущность закона электромагнитной индукции? Предварительно напомним понятие потока электромагнитной индукции. Поток вектора электромагнитной индукции Ф в соответствии с определением потока (любого) вектора записывается в виде
где Ф – поток вектора, Магнитный поток измеряется в веберах (Вб). Из формулы (1.50) видно, что поток вектора магнитной индукции можно изменить тремя способами, связанными с изменением: - модуля вектора магнитной индукции - площади контура; - угла между направлением вектора Все рассмотренные способы приводят к изменению магнитного потока Фундаментальный закон электромагнитной индукции устанавливает связь между изменяющимся магнитным потоком и возникающим электрическим полем. Пусть имеется изменяющееся магнитное поле, причем его изменение связано непосредственно с изменением вектора магнитной индукции
Рис. 1.14. Замкнутый контур в магнитном поле
В курсе общей физики закон электромагнитной индукции записывается в виде:
где В интегральной форме закон электромагнитной индукции имеет вид
где Циркуляция вектора напряженности электрического поля, т. е. Для вывода закона электромагнитной индукции в дифференциальной форме необходимо воспользоваться теоремой Стокса, в результате применения которой интеграл по длине контура преобразуют в интеграл по площади:
Закон электромагнитной индукции можно записать в виде
Так как взят произвольный контур, то интегралы будут равны, если подынтегральные выражения равны, т. е.
Формула (1.53) выражает дифференциальную форму закона электромагнитной индукции, которая указывает на связь между электрическим и магнитным полями в каждой точке пространства. Оператор Таким образом, закон электромагнитной индукции выражает фундаментальную связь между изменением магнитного поля в пространстве с течением времени и возникновением электрического поля. Рассмотрим несколько примеров. Пример 1. Пусть электрическое поле отсутствует, т.е. напряженность электрического поля Пример 2. Пусть имеется изменяющееся магнитное поле. Это означает, что Таким образом, изменение во времени магнитного поля приводит к возникновению электрического поля. Пример 3. Определим связь между направлениями силовых линий электрического и магнитного полей. Пусть имеется изменяющееся магнитное поле, как показано на рис. 1.15. В первом случае (рис. 1.15а) поле возрастает, во втором (рис. 1.15б) – убывает.
Рис. 1.15. Направление силовых линий наведенного магнитного поля
Поместим замкнутый контур в такое изменяющееся магнитное поле. Так как магнитный поток, пересекающий контур, изменяется, то возникает электрическое поле напряженностью Подчеркнем, что наличие проводящего контура не является обязательным. Ток, индуцированный в проводящем контуре, возникает в результате силового действия напряженности электрического поля на свободные заряды, существующие в проводнике. Возникновение самого электрического поля не связано с наличием реального контура. Если отсутствует контур, то электрическое поле возникает не только в вакууме, но и в любой другой среде. Именно такую закономерность утверждает закон электромагнитной индукции. Электрическое поле, порождаемое переменным магнитным полем, является вихревым, а силовые линии такого поля – замкнутыми. Уравнения Максвелла, выражающие закон электромагнитной индукции в интегральной и дифференциальной формах, содержат характеристики магнитного и электрического полей. Иными словами, уравнения Максвелла никак не связаны с материальным контуром, они выражают обобщенный характер выявленных закономерностей. Уравнения Максвелла описывают поле в данном месте пространства в конкретный момент времени. Переменное магнитное поле создает вокруг себя вихревое электрическое поле.
|


 , (1.50)
, (1.50) , (1.50)
, (1.50) – индукция магнитного поля,
– индукция магнитного поля,  – направленная площадка, ограниченная контуром,
– направленная площадка, ограниченная контуром,  – нормаль, проведенная к площадке
– нормаль, проведенная к площадке  ,
,  – угол между направлениями вектора индукции магнитного поля
– угол между направлениями вектора индукции магнитного поля  , т.е. изменением численного значения индукции поля;
, т.е. изменением численного значения индукции поля; и нормали
и нормали  .
. (рис. 1.14).
(рис. 1.14).
 , (1.51)
, (1.51) – ЭДС индукции,
– ЭДС индукции, 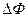 – изменение потока магнитной индукции,
– изменение потока магнитной индукции,  – время, в течение которого произошло изменение магнитного потока. Знак минус выражает правило Ленца, указывающее на противодействующий характер магнитного поля, возникающего вследствие индукции по отношению к внешнему магнитному полю.
– время, в течение которого произошло изменение магнитного потока. Знак минус выражает правило Ленца, указывающее на противодействующий характер магнитного поля, возникающего вследствие индукции по отношению к внешнему магнитному полю.
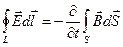 , (1.52)
, (1.52) – напряженность электрического поля,
– напряженность электрического поля, 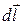 – направленный элемент длины проводника,
– направленный элемент длины проводника,  , выражает собой возникающую в контуре электродвижущую силу (ЭДС), под действием которой появляется электрический ток. Отметим, что контур может быть как мысленно рассматриваемый, так и реально взятый в виде замкнутого проводника.
, выражает собой возникающую в контуре электродвижущую силу (ЭДС), под действием которой появляется электрический ток. Отметим, что контур может быть как мысленно рассматриваемый, так и реально взятый в виде замкнутого проводника. .
. .
.
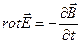 . (1.53)
. (1.53) содержит только пространственные производные, член
содержит только пространственные производные, член  в правой части формулы (1.53) выражает производную по времени. Отсюда видно, что характер изменения напряженности магнитного поля
в правой части формулы (1.53) выражает производную по времени. Отсюда видно, что характер изменения напряженности магнитного поля  . Тогда
. Тогда 
 и
и  . Равенство производной нулю означает, что магнитная индукция
. Равенство производной нулю означает, что магнитная индукция 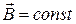 . Полученные выражения показывают, что в отсутствие электрического поля магнитное поле может быть только постоянным.
. Полученные выражения показывают, что в отсутствие электрического поля магнитное поле может быть только постоянным. и
и  , т. е. существует производная по времени. Тогда согласно закону электромагнитной индукции
, т. е. существует производная по времени. Тогда согласно закону электромагнитной индукции 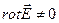 . Отсюда следует, что
. Отсюда следует, что 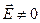 .
.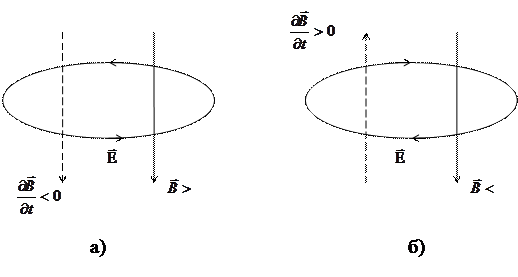
 сонаправлены, силовые линии напряженности электрического поля имеют направление против часовой стрелки; в случае, изображенном на рис. 1.15б, векторы
сонаправлены, силовые линии напряженности электрического поля имеют направление против часовой стрелки; в случае, изображенном на рис. 1.15б, векторы 


