Закон Гаусса
Закон Гаусса устанавливает связь между электрическим зарядом и напряженностью электрического поля Пусть внутри некоторого объема V, имеющего поверхность S, заключен суммарный электрический заряд qS (рис. 1.3).
Рис. 1.3. Заряд, заключенный внутри объема V
Предварительно введем понятие потока вектора напряженности электрического поля в виде скалярного произведения двух векторов
Для пояснения содержания понятия потока вектора напряженности электрического поля
Рис. 1.4. Две параллельные заряженные плоскости
Пусть в пространстве между плоскостями расположена элементарная площадка Если изменить ориентацию площадки таким образом, что
т.е. поток вектора Рис. 1.4 отражает случай максимального значения потока вектора напряженности электрического поля, т.к. векторы Можно заключить, что понятие потока вектора показывает количество линий, пересекающих рассматриваемую поверхность. Закон Гаусса математически записывают в виде
где Скалярное произведение Закон Гаусса можно записать с помощью вектора индукции электрического поля. Для этого уравнение (1.28) нужно несколько видоизменить, освободившись от знаменателя, т.е.
но так как
Закон, записанный с помощью интеграла вдоль замкнутой поверхности, называется законом Гаусса в интегральной форме. Такая форма указывает на выполнение закона в целом, независимо от свойств среды. Заряды, как вы знаете, бывают положительные и отрицательные. Кроме того, нормаль к поверхности проводится внешняя (рис. 1.5). Для расчета потока вектора
а) б) в) Рис. 1.5. Примеры определения потока вектора напряженности электрического поля
Если заряд отрицательный, то угол Часто необходимо знать проявление закона в конкретных точках рассматриваемого пространства. Для этого заменим интеграл по поверхности через интеграл по объему на основе известного соотношения векторного анализа:
Таким образом, левую часть формулы (1.28) преобразовали, заменив интеграл по поверхности на интеграл по объему. Правую часть
Тогда от интегральной формы записи закона перейдем к дифференциальной форме
Формулу (1.35) можно также записать в виде
т.е. пришли к формуле:
Формулы (1.35) и (1.37) называют законом Гаусса в дифференциальной форме. Физически эти соотношения означают, что источниками электрического поля являются только электрические заряды. Иными словами, электрическое поле порождается электрическими зарядами. Подчеркнем, что нормаль к элементу
Рис. 1.6. Расположение внешней нормали к произвольной поверхности
Заряд в объеме может быть расположен произвольным образом. Кроме того, заряд внутри объема может изменяться с течением времени по произвольному закону. Как известно, оператор дивергенции определяется как Дивергенция является пределом отношения потока вектора через замкнутую поверхность S к величине объема V, ограниченной этой поверхностью. Дивергенция отлична от нуля, если силовые линии поля начинаются или заканчиваются в данной точке. Закон Гаусса указывает, что силовые линии поля могут начинаться или заканчиваться только в точках пространства, где существуют заряды. Если во всех точках рассматриваемой области заряд отсутствует, т.е. q = 0, то силовые линии поля пронизывают эту область насквозь либо являются замкнутыми. Таким образом, положительный заряд, расположенный в точке пространства, является «истоком» векторного электрического поля. Если заряд отрицательный, т.е. q<;0, то
Рис. 1.7. К определению понятия дивергенция
Закон Гаусса является фундаментальным, из него можно получить аналитическое выражение закона Кулона.
|

 , которое он порождает.
, которое он порождает.

 . (1.26)
. (1.26)
 , которая может принимать любую ориентацию. Очевидно, если вектор нормали, проведенный к площадке, сонаправлен (параллелен) вектору
, которая может принимать любую ориентацию. Очевидно, если вектор нормали, проведенный к площадке, сонаправлен (параллелен) вектору  ), то площадку
), то площадку  , т.е. угол между нормалью и направлением вектора
, т.е. угол между нормалью и направлением вектора  , (1.27)
, (1.27) и
и 
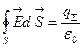 , (1.28)
, (1.28) – суммарный заряд, заключенный внутри поверхности S,
– суммарный заряд, заключенный внутри поверхности S,  – диэлектрическая постоянная.
– диэлектрическая постоянная. представляет собой поток вектора напряженности электрического поля, проходящий через площадку
представляет собой поток вектора напряженности электрического поля, проходящий через площадку  означает, что рассматриваем полный поток вектора через всю замкнутую поверхность.
означает, что рассматриваем полный поток вектора через всю замкнутую поверхность. , (1.29)
, (1.29) , (1.30)
, (1.30) можно записать
можно записать . (1.31)
. (1.31) > 0, значит
> 0, значит  > 0 (рис. 1.5а).
> 0 (рис. 1.5а).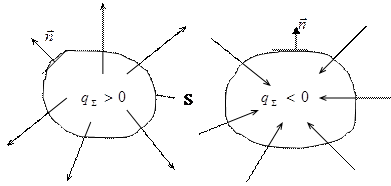

 .. (1.32)
.. (1.32) . (1.33)
. (1.33)
 . (1.34)
. (1.34) Так как мы рассматриваем произвольный объем, то последнее равенство выполняется, если подынтегральные выражения равны между собой. Тогда можно записать
Так как мы рассматриваем произвольный объем, то последнее равенство выполняется, если подынтегральные выражения равны между собой. Тогда можно записать . (1.35)
. (1.35)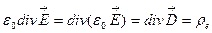 , (1.36)
, (1.36)
 . (1.37)
. (1.37) , выделенному по поверхности объема, проводится внешняя (рис. 1.6).
, выделенному по поверхности объема, проводится внешняя (рис. 1.6).
 .
. . Такая точка пространства является «стоком» векторного электрического поля. На рис. 1.7 приведены соответствующие графические пояснения
. Такая точка пространства является «стоком» векторного электрического поля. На рис. 1.7 приведены соответствующие графические пояснения



