Материальные уравнения электромагнитного поля для вакуума
Рассмотренные выше четыре уравнения Максвелла образуют фундаментальную систему уравнений электродинамики. Такая система уравнений справедлива для любой среды, в которой происходит распространение полей. Однако, чтобы система уравнений была полной и однозначно определяла поле в любой точке среды, необходимо добавить уравнения, учитывающие свойства самой среды, которые проявляются в характере связи между характеристиками поля, то есть между Среду, в которой происходят электрические и магнитные явления, характеризуют диэлектрической проницаемостью В вакууме материальные уравнения имеют вид:
С точки зрения способности проводить электрический ток все среды делят на проводники, диэлектрики и полупроводники. Проводники – это вещества, способные проводить электрический ток и обладающие удельной проводимостью Диэлектрики – это вещества, не способные проводить электрический ток. Диэлектрики характеризуются удельной проводимостью
Рис. 1.16. Классификация сред по способности проводить электрический ток Полупроводники – это вещества, которые обладают одновременно свойствами проводника и диэлектрика. Для полупроводников удельная проводимость изменяется в пределах Во многих задачах электродинамики реальные проводники и диэлектрики удобно заменить идеальными проводниками и диэлектриками. В этом случае для идеального проводника принимаем σ=∞, идеального диэлектрика Поведение проводников в электрическом поле рассмотрено выше, где выяснено, что под действием внешнего электрического поля в проводнике наводится ток проводимости в соответствии с дифференциальным законом Ома, т.е.
|

 и
и  ,
,  и
и  . Уравнения, устанавливающие связь между указанными характеристиками поля с учетом свойств среды, называются материальными уравнениями.
. Уравнения, устанавливающие связь между указанными характеристиками поля с учетом свойств среды, называются материальными уравнениями. , магнитной проницаемостью
, магнитной проницаемостью  и удельной проводимостью σ.
и удельной проводимостью σ.
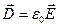 ,
,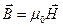 , (1.54)
, (1.54)  – диэлектрическая постоянная,
– диэлектрическая постоянная, 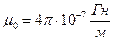 – магнитная постоянная.
– магнитная постоянная.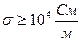 (сименс на метр).
(сименс на метр).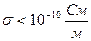 .
.
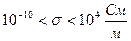 . На рис. 1.16 показано разделение веществ по значению удельной проводимости.
. На рис. 1.16 показано разделение веществ по значению удельной проводимости.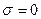 .
. . Влиянием магнитного поля пренебрегаем.
. Влиянием магнитного поля пренебрегаем.


