Уравнения Максвелла в комплексной форме
Выше указывалось, что уравнения Максвелла в дифференциальной форме описывают электромагнитные процессы в пространстве и во времени. Иными словами, в описании процесса используют три пространственные координаты, а четвертой переменной является время, т. е. необходимо наличие четырех переменных ( Систему уравнений Максвелла можно записать в иной форме, позволяющей «избавиться» от временной переменной и рассматривать электромагнитный процесс, протекающий в пространстве, с помощью трех переменных – координат ( Рассмотрим более подробно вывод новой формы записи уравнений Максвелла. Примем, что сторонние токи отсутствуют. Уравнения Максвелла в дифференциальной форме в этом случае записывают в виде
Такая система уравнений записана для мгновенных значений
где Мгновенные значения напряженности полей (1.75) можно записать в виде
где
где Так как напряженности полей являются векторными величинами, будем обозначать их
Плотность тока смещения представим в виде:
Тогда исходное уравнение Максвелла
После сокращения получаем формулу
Таким образом, получено уравнение Максвелла в комплексной форме записи. Сформулируем правило перехода дифференциальной формы уравнений Максвелла к комплексной форме: оператор дифференцирования по времени, действующий на мгновенное значение поля, заменяется на множитель Аналогично можно преобразовать остальные уравнения системы. В результате система уравнений Максвелла в комплексной форме записи имеет вид:
Таким образом, система уравнений Максвелла имеет три формы записи: интегральную, дифференциальную, комплексную.
|

 ). Мы учли, что используем декартову систему координат. Описать процесс при наличии четырех переменных достаточно сложно.
). Мы учли, что используем декартову систему координат. Описать процесс при наличии четырех переменных достаточно сложно. ).
).
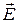 и
и  . Для гармонически изменяющихся во времени
. Для гармонически изменяющихся во времени  и
и  запишем
запишем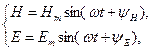 (1.75)
(1.75) – амплитудные значения,
– амплитудные значения, 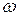 – угловая частота,
– угловая частота,  – время,
– время,  – начальные фазы.
– начальные фазы. , (1.76)
, (1.76) – это мнимая часть. Тогда для мгновенных значений напряженностей полей запишем
– это мнимая часть. Тогда для мгновенных значений напряженностей полей запишем ,
, ,
,  .
.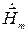 и
и  . Стрелка означает, что речь идет о векторе в пространстве, точка – о том, что проекция вектора на любую координатную ось изменяется с течением времени по синусоидальному закону. Учитывая введенные обозначения, можно для плотности тока проводимости записать:
. Стрелка означает, что речь идет о векторе в пространстве, точка – о том, что проекция вектора на любую координатную ось изменяется с течением времени по синусоидальному закону. Учитывая введенные обозначения, можно для плотности тока проводимости записать: .
. ,
,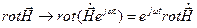 .
. перепишем в виде
перепишем в виде .
.
 . (1.77)
. (1.77) .
.
 ,
, ,
, ,
, , (1.78)
, (1.78) ,
,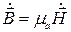 .
.


