Граничные условия для нормальных составляющих электрического поля
Аналогично методике, примененной в предыдущем параграфе, выведем граничные условия для нормальных составляющих электрического поля. Поток вектора индукции через суммарную поверхность запишется суммой произведения индукции электрического поля
Напомним, что в случае электрического поля выполняется равенство:
В рассматриваемом случае возможны два варианта: 1. Плотность поверхностных электрических зарядов равна нулю, т.е. s = 0. В соответствии с теоремой Гаусса суммарный заряд, заключенный в рассматриваемой цилиндрической поверхности, будет равен
Отсюда можно записать
Поскольку
запишем граничные условия для нормальных составляющих векторов напряженности электрического поля
Таким образом, при отсутствии поверхностных электрических зарядов на границе раздела двух сред нормальные составляющие индукции электрического поля будут непрерывны, а нормальные составляющие векторов напряженности электрического поля будут испытывать скачок. 2. На границе раздела равномерно распределен поверхностный электрический заряд, который имеет плотность s. Используя закон Гаусса и устремив образующую цилиндра к нулю, можно записать формулу:
Отсюда получим формулу в виде
Это означает, что при наличии заряженной границы раздела двух сред нормальные составляющие индукции электрического поля испытывают скачок на величину плотности поверхностного заряда.
|
на площадь верхнего и нижнего оснований выделенного цилиндра и потока через боковую поверхность:
поток через боковую поверхность. (2.5)
.
. (2.6)
.
,
. (2.7)
. (2.8)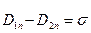
.
