Общие свойства волновых процессов
Прежде чем рассматривать волновой процесс, дадим определение колебательного движения. Колебание – это периодически повторяющийся процесс. Примеры колебательных движений весьма разнообразны: смена сезонов года, колебание сердца, дыхание, заряд на обкладках конденсатора и другие. Уравнение колебания A(t) в общем виде записывают в виде
где От колебательного движения перейдем к рассмотрению волнового движения. Волна – это процесс распространения колебаний в пространстве с течением времени. Так как колебания распространяются в пространстве с течением времени, то в уравнении волны необходимо учесть пространственные координаты и время. Уравнение волны A(z,t) имеет вид
где А0 – амплитуда, w – частота, t – время, b – волновое число, z – координата. Физическая природа волн весьма многообразна. Известны звуковые, электромагнитные, гравитационные, акустические волны. По типу колебаний все волны классифицируют на продольные и поперечные. Продольные волны – это волны, у которых частицы среды колеблются вдоль направления распространения волны. Примером продольной волны является звуковая волна.
а б Рис. 3.1. Продольные (а) и поперечные (б) волны
Поперечные волны – это волны, у которых частицы среды колеблются в поперечном направлении относительно направления распространения. Электромагнитные волны относятся к поперечным волнам. Следует учесть, что в электромагнитных волнах происходит колебание поля и не происходит никакого колебания частиц среды. Если в пространстве происходит распространение волны с одной частотой w, то такая волна называется монохроматической. Для описания распространения волновых процессов вводят следующие характеристики. Аргумент косинуса (см. формулу (3.2)), т.е. выражение Схематически распространение волны вдоль одной координаты показано на рис. 3.2, в данном случае – вдоль оси z.
Рис. 3.2. Определение длины волны
Период – время одного полного колебания. Период обозначается буквой Т и измеряется в секундах (с). Величина, обратная периоду, называется линейной частотой, обозначается f и измеряется в герцах (
Если зафиксировать время t, то из рис. 3.2 видно, что существуют точки, например А и В, которые колеблются одинаково, т.е. в фазе (синфазно). Расстояние между ближайшими двумя точками, колеблющимися в фазе, называется длиной волны. Обозначается длина волны l и измеряется в метрах (м). Волновое число b и длина волны l связаны между собой формулой
Волновое число b иначе называют фазовой постоянной или постоянной распространения. Из формулы (3.4) видно, что постоянная распространения измеряется в ( Для описания волнового процесса вводят понятие фронта волны. Фронт волны – это геометрическое место воображаемых точек поверхности, до которых дошло возбуждение. Фронт волны иначе называют волновым фронтом. Уравнение, описывающее волновой фронт плоской волны, получают из уравнения (3.2) в виде
Формула (3.5) выражает уравнение волнового фронта плоской волны. Уравнение (3.4) показывает, что волновые фронты представляют собой бесконечные плоскости, перемещающиеся в пространстве перпендикулярно оси z. Скорость перемещения фазового фронта называется фазовой скоростью. Фазовая скорость обозначается Vф и определяется формулой
Первоначально уравнение (3.2) содержит фазу с двумя знаками – отрицательным и положительным. Отрицательный знак, т.е. Положительный знак фазы волны указывает на движение фронта волны в обратном направлении, т.е. противоположном направлению оси z. Такая волна называется отраженной. В дальнейшем будем рассматривать бегущие волны. Если волна распространяется в реальной среде, то из-за происходящих тепловых потерь неизбежно происходит уменьшение амплитуды. Рассмотрим пример. Пусть волна распространяется вдоль оси z и первоначальное значение амплитуды волны соответствует 100%, т.е. A0=100. Допустим, при прохождении одного метра пути амплитуда волны уменьшается на 10%. Тогда будем иметь следующие значения амплитуд волн:
Общая закономерность изменения амплитуды имеет вид
Такими свойствами обладает показательная функция. Графически процесс можно показать в виде рис. 3.3.
Рис. 3.3. Уменьшение амплитуды при распространении волны в среде
В общем виде соотношение пропорциональности запишем как
где a – постоянная затухания волны. Фазовую постоянную b и постоянную затухания a объединяют с помощью введения комплексной постоянной распространения g, т.е.
где b – фазовая постоянная, a – постоянная затухания волны. В зависимости от вида волнового фронта различают волны плоские, сферические, цилиндрические. Плоская волна – это волна, имеющая плоский фронт. Плоской волне можно дать следующее определение. Волна называется плоской однородной, если векторные поля Уравнение плоской волны имеет вид:
Если источник, порождающий волну, является точечным, то фронт волны, распространяющийся в неограниченном однородном пространстве, представляет собой сферу. Сферическая волна – это волна, имеющая сферический фронт. Уравнение сферической волны имеет вид
где r – радиус-вектор, проведенный из начала координат, совпадающего с положением точечного источника, в конкретную точку пространства, расположенной на расстоянии r. Волны могут возбуждаться с помощью бесконечной нити источников, расположенных вдоль оси z. В этом случае такая нить будет порождать волны, фазовый фронт которых представляет собой цилиндрическую поверхность. Цилиндрическая волна – это волна, имеющая фазовый фронт в виде цилиндрической поверхности. Уравнение цилиндрической волны имеет вид
Формулы (3.2), (3.10), (3.11) указывают на различную зависимость амплитуды от расстояния между источником волны и конкретной точкой пространства, до которой дошла волна.
|


 , (3.1)
, (3.1) – амплитуда колебаний,
– амплитуда колебаний, 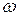 – циклическая частота,
– циклическая частота,  – время,
– время,  – начальная фаза. Часто начальную фазу принимают равной нулю.
– начальная фаза. Часто начальную фазу принимают равной нулю. , (3.2)
, (3.2)
 , называется фазой волны.
, называется фазой волны.
 =Гц). Линейная частота f связана с круговой частотой ω;. Связь выражается формулой
=Гц). Линейная частота f связана с круговой частотой ω;. Связь выражается формулой . (3.3)
. (3.3) . (3.4)
. (3.4) ). Физический смысл заключается в том, что она показывает, на сколько радиан изменяется фаза волны при прохождении одного метра пути.
). Физический смысл заключается в том, что она показывает, на сколько радиан изменяется фаза волны при прохождении одного метра пути.
 . (3.5)
. (3.5)
 . (3.6)
. (3.6) , указывает, что фронт волны распространяется вдоль положительного направления распространения оси z. Такая волна называется бегущей, или падающей.
, указывает, что фронт волны распространяется вдоль положительного направления распространения оси z. Такая волна называется бегущей, или падающей.
 .
.
 , (3.7)
, (3.7)
 , (3.8)
, (3.8)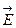 и
и 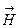 в любой точке плоскости перпендикулярны направлению распространения и не изменяются по фазе и амплитуде.
в любой точке плоскости перпендикулярны направлению распространения и не изменяются по фазе и амплитуде. . (3.9)
. (3.9) , (3.10)
, (3.10) , (3.11)
, (3.11)


