Распространение плоских электромагнитных волн в хорошо проводящих средах
Формула (3.66) выражает условие, при котором реальную среду можно считать проводящей. Иными словами, мнимая часть комплексной диэлектрической проницаемости должна превосходить действительную часть. Формула (3.66) также показывает зависимость Для реальной среды запишем комплексную диэлектрическую проницаемость
В нашем случае
Постоянная распространения g, как известно, определяется из уравнений Гельмгольца
Таким образом, получим формулу для постоянной распространения
Известно, что
Учитывая тождество (3.49), формулу (3.50) запишем в виде
Постоянная распространения выражается в виде
Сравнение действительных и мнимых частей в формулах (3.71), (3.72) приводит к равенству значений фазовой постоянной b и постоянной затухания a, т.е.
Из формулы (3.73) выпишем длину волны, которую приобретает поле при распространении в хорошо проводящей среде:
где Из полученной формулы (3.74) видно, что длина электромагнитной волны, распространяющейся в металле, значительно сокращается по сравнению с длиной волны в пространстве. Выше сказано, что амплитуда волны при распространении в среде с потерями уменьшается по закону Глубина поверхностного слоя –это расстояние d, на котором амплитуда поверхностной волны уменьшается в е раз по сравнению с ее начальным уровнем.
где
где w – циклическая частота, mа – абсолютная магнитная проницаемость среды, s – удельная проводимость среды. Из формулы (3.76) видно, что с повышением частоты и удельной проводимости глубина поверхностного слоя уменьшается. Приведем пример. Медь с удельной проводимостью
|

 Рассмотрим распространение электромагнитной волны в проводящей среде. Такие среды также называют металлоподобными. Реальная среда является проводящей, если плотность токов проводимости значительно превосходит плотность токов смещения, т.е.
Рассмотрим распространение электромагнитной волны в проводящей среде. Такие среды также называют металлоподобными. Реальная среда является проводящей, если плотность токов проводимости значительно превосходит плотность токов смещения, т.е.  и
и  , причем
, причем  , или
, или . (3.66)
. (3.66) от частоты. Причем чем ниже частота, тем в среде более ярко выражены свойства проводника. Рассмотрим пример. Так, на частоте f = 1МГц = =106 Гц сухая почва имеет параметры e=4, s=0,01
от частоты. Причем чем ниже частота, тем в среде более ярко выражены свойства проводника. Рассмотрим пример. Так, на частоте f = 1МГц = =106 Гц сухая почва имеет параметры e=4, s=0,01  ,. Сравним между собой
,. Сравним между собой  и
и  , т.е
, т.е  и
и  . Из полученных значений видно, что 1,6×10-9 >> 3,56×10-11, поэтому сухую почву при распространении волны с частотой 1 МГц следует считать проводящей.
. Из полученных значений видно, что 1,6×10-9 >> 3,56×10-11, поэтому сухую почву при распространении волны с частотой 1 МГц следует считать проводящей. . (3.67)
. (3.67) . (3.68)
. (3.68) .
. . (3.69)
. (3.69) . (3.70)
. (3.70)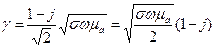 . (3.71)
. (3.71) . (3.72)
. (3.72) . (3.73)
. (3.73) , (3.74)
, (3.74) – длина волны в металле.
– длина волны в металле. . Для характеристики процесса распространения волны в проводящей среде введено понятие глубины поверхностного слоя или глубины проникновения.
. Для характеристики процесса распространения волны в проводящей среде введено понятие глубины поверхностного слоя или глубины проникновения.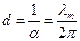 , (3.75)
, (3.75) – длина волны в металле.
– длина волны в металле. Глубину поверхностного слоя также определяют из формулы
Глубину поверхностного слоя также определяют из формулы , (3.76)
, (3.76) на частоте f = 10 ГГц (l = 3см) имеет глубину поверхностного слоя d =
на частоте f = 10 ГГц (l = 3см) имеет глубину поверхностного слоя d =  . Отсюда сделаем важный для практики вывод: нанесение на непроводящее покрытие слоя хорошо проводящего вещества позволит выполнить элементы устройств с малыми тепловыми потерями.
. Отсюда сделаем важный для практики вывод: нанесение на непроводящее покрытие слоя хорошо проводящего вещества позволит выполнить элементы устройств с малыми тепловыми потерями.


