Поляризацией поля на идеально проводящую плоскость
Пусть из вакуума на идеально проводящую плоскость под углом j падает плоская монохроматическая волна, имеющая вертикальную поляризацию (рис. 4.2).
На рис. 4.2 показаны мгновенные положения последовательности волновых фронтов, отстающих друг от друга на расстояние Рис. 4.2. Падающий и отраженный фронты волны
На границе идеального проводника выполняются граничные условия, т.е. 1) модуль коэффициента отражения равен 1, поэтому амплитуды падающей и отраженной волн одинаковы по величине, т.е.
2) на границе раздела выполняются граничные условия, т.е. На рис. 4.2 показан результат сложения полей падающей и отраженной волн. Результат сложения сделан в узлах образующейся сетки волновых поверхностей. Результаты сложения волновых процессов позволяют сделать следующие выводы: 1) суммарные силовые линии магнитного поля имеют вид бесконечных нитей, направленных параллельно оси oy; 2) векторы напряженности электрического поля лежат в плоскости хоz, причем ориентация этих векторов непрерывно меняется от точки к точке. Из рис. 4.2 видно, что силовые линии напряженности суммарного поля имеют определенную закономерность в пространстве. Подчеркнем: в сложении участвовали волновые фронты, положение которых отличалось по фазе на p (противофаза). Если провести более детальное сложение и изобразить результирующее суммарное поле электромагнитной волны с вертикальной поляризацией, то получим картину силовых линий, показанную на рис. 4.3.
Рис. 4.3. Результирующее поле волны Е - типа
На рис. 4.3 видно, что силовые линии напряженности поля Аналогичным образом можно рассмотреть падение плоской электромагнитной волны с горизонтальной поляризацией из воздуха на плоскую проводящую поверхность. Не останавливаясь детально на рассмотрении такого падения электромагнитной волны, покажем результирующее поле с помощью силовой картины, содержащей и суммарный вектор
Рис. 4.4. Результирующее поле волны Н – типа
Электромагнитная волна также распространяется вдоль оси z. Напряженность магнитного поля Из рис. 4.4 видно, что силовые линии Волна Н-типа имеет и другое название: ТЕ, т.е поперечная электрическая волна. Действительно, в волне Н-типа существует поле Мы рассмотрели падение плоской электромагнитной волны с различными поляризациями (горизонтальной и вертикальной) из воздуха на проводящую плоскость. Суммарная (результирующая) волна – результат интерференции плоской падающей и отраженной волны и уже не является плоской. Таким образом, проводящую плоскость следует рассматривать как направляющую, вдоль которой распространяются волны Е- и Н-типов. На границе раздела плоскости с воздухом выполняются граничные условия, т.е.
|


 . Поэтому фазы поля для соседних положений фронтов отличаются на величину 180°. Показаны также взаимные ориентации векторов для падающего фронта волн
. Поэтому фазы поля для соседних положений фронтов отличаются на величину 180°. Показаны также взаимные ориентации векторов для падающего фронта волн  ,
,  .
. . В нашем случае это условие будет выполняться, если будет существовать отраженная волна. На рис. 4.2 показаны поверхности равных фаз для отраженной волны, причем векторы электромагнитного поля отраженной волны, обозначенные
. В нашем случае это условие будет выполняться, если будет существовать отраженная волна. На рис. 4.2 показаны поверхности равных фаз для отраженной волны, причем векторы электромагнитного поля отраженной волны, обозначенные  ,
,  , обладают следующими свойствами:
, обладают следующими свойствами: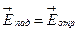 ,
,  .
.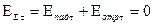 ;
; , где
, где  – суммарные тангенциальные составляющие,
– суммарные тангенциальные составляющие,  –тангенциальные составляющие падающей волны,
–тангенциальные составляющие падающей волны,  – тангенциальные составляющие отраженной волны.
– тангенциальные составляющие отраженной волны.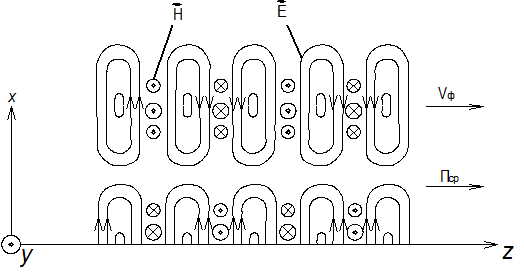
 перпендикулярны металлической поверхности и что в замкнутых линиях
перпендикулярны металлической поверхности и что в замкнутых линиях  имеет только перпендикулярные составляющие, которые являются поперечными направлению распространения волны. Поэтому волны Е-типа называются также ТМ-волнами, т.е. поперечными магнитными волнами.
имеет только перпендикулярные составляющие, которые являются поперечными направлению распространения волны. Поэтому волны Е-типа называются также ТМ-волнами, т.е. поперечными магнитными волнами.



