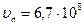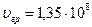Прямоугольный металлический волновод
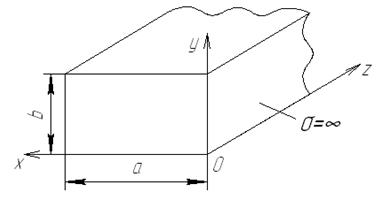
На практике для передачи электромагнитных волн СВЧ-диапазона наиболее часто используют прямоугольные металлические волноводы, представляющие собой полые металлические трубы прямоугольного сечения. На рис. 4.7 схематично изображен прямоугольный металлический волновод.
Рис. 4.7. Схема прямоугольного волновода
Принято размеры широкой стенки волновода обозначать а, узкой стенки b. Таким образом, размеры прямоугольного сечения волновода обозначают ахb. Такое обозначение указано в государственном стандарте (ГОСТ). Размеры волноводов, применяемых в различных диапазонах волн, указаны в справочниках по волноводной технике. С прямоугольными волноводами связывают прямоугольную декартову систему координат (x, y, z). Обычно систему координат размещают так, как показано на рис. 4.7. Широкое применение полых металлических волноводов обусловлено их достоинствами: - высокой технологичностью изготовления; - достаточно малым затуханием энергии при распространении волны; - возможностью передачи значительных мощностей в импульсном режиме. Пусть внутри волновода находится воздух или вакуум (e=1), т.е. для такого волновода параметры среды имеют значения В таких волноводах могут распространяться волны Е- и Н-типов. На практике наибольшее распространение получили волны Н-типа, в частности, основной тип волны – волна Н10. Заметим, волна Н-типа для волновода прямоугольного сечения записывается в виде Нmn, где m, n – индексы, указывающие на количество полуволн вдоль оси х и у соответственно. Исследуем поле Н-волны в прямоугольном волноводе. Напомним, что для такой волны имеются продольные и поперечные составляющие магнитного поля, а продольные составляющие электрического поля равны нулю. Волновое уравнение для составляющей
Решение уравнения Гельмгольца (4.1) имеет вид
где h – продольное волновое число. Волновой процесс происходит одновременно и вдоль оси z, и вдоль перпендикулярной плоскости xoy. Введем соответствующие волновые числа или постоянные распространения: g – постоянная распространения в свободном пространстве, h – продольное волновое число, g – поперечное волновое число. Между волновыми числами существует связь
На основе формулы (4.3) продольное волновое число выразим в виде 1) если g>g, то продольное волновое число является вещественным и это означает, что вдоль оси z распространяется бегущая волна; 2) если g<g, то продольное волновое число h является мнимым и в волноводе нет распространяющихся колебаний. В волновом процессе необходимо различать длину волны генератора l0, или длину волны, распространяющуюся в свободном пространстве. Для описания распространения волны в волноводе введем понятия длины волны в волноводе lв, критической длины волны lкр. Итак следует различать между собой: l0, lв, lкр. Критическая длина волны – это наибольшая длина волны, которая может распространяться в волноводе для данного типа колебаний. Связь между волновыми числами и длинами волн выражается формулами:
Критическая длина волны и длина волны в волноводе определяются формулами:
где m, n – соответствующие индексы волны, a, b – размеры волновода.
где l0 – длина волны генератора, lкр – критическая длина волны. Формулы (4.7) и (4.8) показывают, что для каждого типа волны при соответствующих размерах волновода существует определенная критическая длина волны. Длина волны, распространяющаяся в волноводе, зависит от длины волны в свободном пространстве и критической длины волны. Для волны Нmn справедливы формулы:
где Vф – фазовая скорость, Vгр – групповая скорость, ZОН – волновое сопротивление для волны Н-типа.
4.5. Поле волны Н10 в прямоугольном волноводе
Основным, или низшим, типом волны называется такой тип волны, который обладает наибольшей критической длиной волны при данных размерах волновода. Поперечные размеры волновода для заданной частоты берутся наименьшие. В прямоугольном волноводе низшим типом волны является волна Н10. Для такой волны критическая длина имеет значение
Передачу энергии по прямоугольному волноводу часто производят с помощью волны Н10. Структура поля волны Н10 описывается формулами:
Поперечное волновое число g определяется формулой
Формулы (4.13), описывающие структуру поля волны Н10, можно записать в вещественном виде, позволяющем более просто описать электромагнитное поле.
Структура поля волны Н10 в виде силовых линий показана на рис. 4.8.
Рис. 4.8. Структура поля волны Н10
Фазовая скорость распространения волны Н10 в волноводе определяется как
где Z0 – волновое сопротивление среды, заполняющей волновод, Магнитное поле, как следует из формул (4.13), (4.15), имеет две составляющие, амплитуды которых зависят от координат рассматриваемой точки. Эти составляющие сдвинуты в пространстве и времени на 90°. Отсюда видно, что магнитное поле волны Н10 имеет эллиптическую поляризацию. Внутри волновода выполняются условия для протекания поверхностного тока, плотность которого определяется формулой
Рис. 4.9. Картина поверхностных токов на стенках волновода
Определим мощность, переносимую основным типом волны Н10. Значение модуля вектора Пойнтинга определяется формулой
Тогда мощность, переносимая через поперечное сечение волновода с учетом усреднения во времени, определяется формулой
где
При заданных размерах волновода диапазон рабочих длин волн определяется соотношением
В прямоугольном волноводе также существуют волны Е-типа, в которых имеются и продольная, и поперечная составляющие поля. Так как волна распространяется вдоль оси z, то уравнение Гельмгольца для составляющей EZ имеет вид
Решение уравнения Гельмгольца с учетом выполнения граничных условий имеет вид
Отметим, что для Е-волн в волноводе можно записать Emn, где индексы m, n определяют конкретную структуру поля. Для Е-волн ни одно из чисел m, n не может быть равно нулю, в противном случае составляющая EZ=0, а следовательно, и другие составляющие поля обратятся в нуль. Таким образом, волны Е-типа вида Е0n и Em0 в прямоугольном волноводе не существуют. В таблице 4.1 показана структура поля волн Е- и Н-типа в прямоугольном волноводе и приведены формулы, определяющие их основные характеристики.

Приведем пример расчета параметров волны, распространяющейся в прямоугольном волноводе. Прямоугольный волновод, заполненный воздухом, имеет поперечное сечение Решение 1. Определяем длину волны в свободном пространстве:
Зная, что скорость света с=3×108 м/с, находим 2. Критическую длину волны в волноводе определяем по формуле:
По волноводу могут распространяться волны, которые удовлетворяют условию
Придавая
т.е. требуемое неравенство (
Для волны типа
|

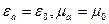 , а его стенки выполнены из идеального проводника, т.е. удельная проводимость s = ¥.
, а его стенки выполнены из идеального проводника, т.е. удельная проводимость s = ¥.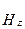 имеет вид
имеет вид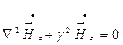 . (4.1)
. (4.1)
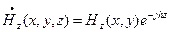 , (4.2)
, (4.2)
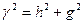 . (4.3)
. (4.3)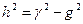 . Из полученной формулы выявим важную особенность, позволяющую понять процесс распространения волны в волноводе:
. Из полученной формулы выявим важную особенность, позволяющую понять процесс распространения волны в волноводе:
 , (4.4)
, (4.4)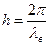 , (4.5)
, (4.5)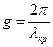 . (4.6)
. (4.6)
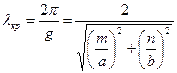 , (4.7)
, (4.7)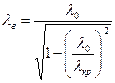 , (4.8)
, (4.8)
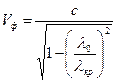 , (4.9)
, (4.9)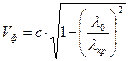 , (4.10)
, (4.10)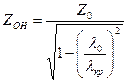 , (4.11)
, (4.11)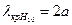 . (4.12)
. (4.12)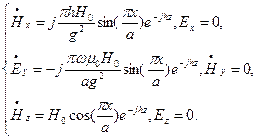 (4.13)
(4.13)
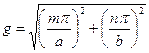 . (4.14)
. (4.14)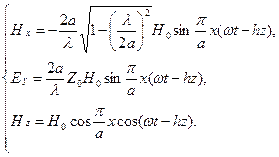 (4.15)
(4.15)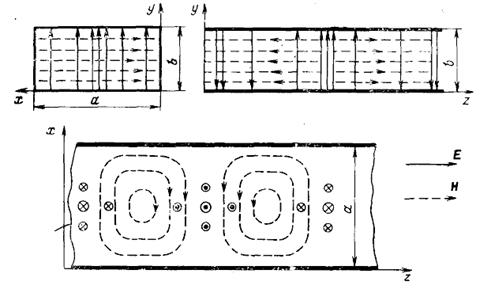
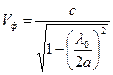 . (4.16)
. (4.16) Длина волны в волноводе отличается от длины волны в свободном пространстве и определяется по формуле
Длина волны в волноводе отличается от длины волны в свободном пространстве и определяется по формуле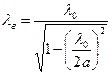 . (4.17)
. (4.17)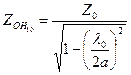 , (4.18)
, (4.18)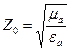 .
.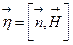 . Картина поверхностных токов приведена на рисунке 4.9.
. Картина поверхностных токов приведена на рисунке 4.9.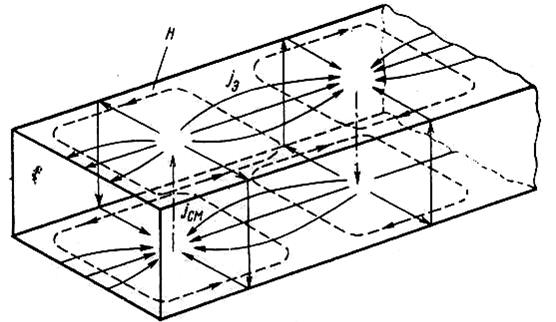
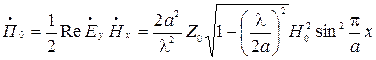 . (4.19)
. (4.19)
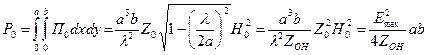 , (4.20)
, (4.20)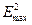 – максимальная амплитуда электрического поля при
– максимальная амплитуда электрического поля при 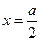 ,
, . (4.21)
. (4.21)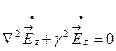 . (4.22)
. (4.22)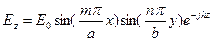 . (4.23)
. (4.23)




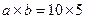
 . Определить все типы волн, которые могут существовать в волноводе при частоте 5000 МГц. Для основной волны и для волны с наиболее высокими значениями
. Определить все типы волн, которые могут существовать в волноводе при частоте 5000 МГц. Для основной волны и для волны с наиболее высокими значениями 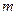 и
и 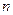 найти критическую длину волны в волноводе, фазовую и групповую скорости.
найти критическую длину волны в волноводе, фазовую и групповую скорости.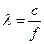 .
.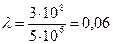 м.
м. .
.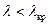 , т.е. в нашем случае
, т.е. в нашем случае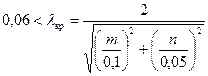 .
.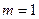 и
и 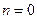 получим
получим 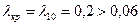 м, т.е. в волноводе может существовать волна типа
м, т.е. в волноводе может существовать волна типа 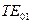 . Аналогично определяем, что по волноводу могут распространяться также волны типа
. Аналогично определяем, что по волноводу могут распространяться также волны типа 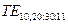 и
и 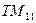 . Других типов волн в волноводе быть не может. Действительно, пусть
. Других типов волн в волноводе быть не может. Действительно, пусть 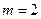 и
и 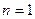 . Тогда получим
. Тогда получим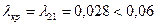 ,
,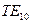 и
и 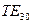 находим длину волны в волноводе, её фазовую и групповую скорости. Для волн типа
находим длину волны в волноводе, её фазовую и групповую скорости. Для волн типа 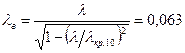
 ,
,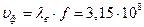
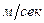 ,
,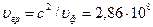
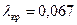
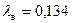 ,
,