Нахождение резонансных частот в объемном резонаторе
Явление резонанса в объемном резонаторе наступает в случае, когда на данной частоте энергия электрического поля равна энергии магнитного поля. Математически равенство энергии полей записывается в виде:
где Первое уравнение Максвелла, как известно, имеет вид:
где Учитывая условие появления резонанса (4.50) и первое уравнение Максвелла, определим собственную частоту колебаний резонатора. Из первого уравнения Максвелла выразим напряженность электрического поля:
Далее подставим уравнение (4.51) в формулу (4.50) и получим:
или запишем уравнение в следующем виде:
Если среда, заполняющая резонатор, не обладает проводящими свойствами, то
Формула (4.52) позволяет определить собственную резонансную частоту электромагнитных колебаний в объемном резонаторе и понять, что собственная резонансная частота зависит от размеров резонатора, свойств заполняющей резонатор среды и от структуры электромагнитного поля. Отсюда следует, что перестройку резонансной частоты можно выполнить с помощью изменения объема резонатора или заполняющей его среды. Изменить объем можно с помощью укорочения или удлинения резонатора, т.е. за счет изменения длины. Также объем резонатора уменьшится, если внутри полости поместить металлическое тело. Итак, изменение объема резонатора возможно двумя способами: изменением объема и заполняющей средой, и оно приводит к изменению резонансной частоты объемного резонатора. Если в полость резонатора поместить диэлектрик, имеющий определенное значение Собственную добротность резонатора определяют, исходя из энергетического соотношения:
где Получение высокой добротности (т.е. большого значения) является важным достоинством объемных резонаторов. Так, резонаторы, изготовленные из хорошо проводящего материала, имеют добротность
|

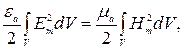 (4.50)
(4.50)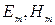 – амплитудные значения, соответственно, электрического и магнитного полей, V – объем, занимаемый полем в резонаторе,
– амплитудные значения, соответственно, электрического и магнитного полей, V – объем, занимаемый полем в резонаторе, 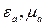 – абсолютная диэлектрическая и магнитная проницаемость среды, заполняющей резонатор.
– абсолютная диэлектрическая и магнитная проницаемость среды, заполняющей резонатор.
 – амплитуда напряженности электрического и магнитного полей,
– амплитуда напряженности электрического и магнитного полей, 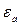 – абсолютная диэлектрическая проницаемость,
– абсолютная диэлектрическая проницаемость,  – комплексная абсолютная диэлектрическая проницаемость, σ; – удельная проводимость вещества.
– комплексная абсолютная диэлектрическая проницаемость, σ; – удельная проводимость вещества.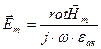 . (4.51)
. (4.51)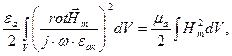
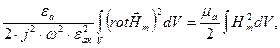
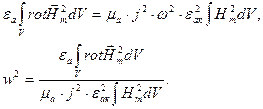
 . Кроме того, физически циклическая частота может принимать положительные значения, поэтому необходимо взять модуль полученного отношения. Учитывая сказанное выше, получим:
. Кроме того, физически циклическая частота может принимать положительные значения, поэтому необходимо взять модуль полученного отношения. Учитывая сказанное выше, получим:
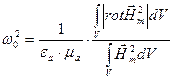 . (4.52)
. (4.52)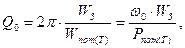 (4.53)
(4.53)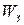 – энергия, запасенная в резонаторе,
– энергия, запасенная в резонаторе,  – энергия, теряемая в резонаторе за один период колебаний,
– энергия, теряемая в резонаторе за один период колебаний, 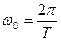 – собственная резонансная круговая частота резонатора,
– собственная резонансная круговая частота резонатора, 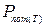 – мощность потерь в резонаторе.
– мощность потерь в резонаторе.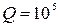 .
.


