Распространение радиоволн в свободном пространстве
Пусть в свободном пространстве (однородной непоглощающей среде с ε=1, μ=1) помещен точечный излучатель, к которому подведена мощность
Рис. 5.4. Сферический фронт волны от точечного излучателя
После начала излучения волны радиус сферического фронта будет иметь значение r. Распространяясь, волна переносит энергию, плотность потока которой через единичную площадку за единицу времени (модуль вектора Пойнтинга) определяется формулой:
где Среднее значение плотности потока энергии за период времени Т определяют из формулы:
где Связь между действующими значениями напряженностей электрического и магнитного полей выражается формулой:
где
Исходя из формул (5.2, 5.3), для модуля вектора Пойнтинга можно записать:
В нашем случае речь идет об одном и том же процессе излучения электромагнитной энергии точечным источником, поэтому на основании (5.1) и (5.4) запишем равенство:
Из равенства (5.5) определим:
где В реальных условиях трассы в пунктах передачи используют антенны, предназначенные для концентрации излучаемой энергии в определенном направлении, т.е. служащие направленному излучению волны. Для учета направленных свойств антенны ввели параметр – коэффициент направленного действия (КНД), выражающий степень направленности. Обозначим КНД через D. Все параметры, относящиеся к передающим устройствам, будем снабжать индексом 1, к приемным устройствам – индексом 2. Например, мощность, подводимую к излучающей антенне в пункте передачи, обозначим Р1, коэффициент ее направленности – D1. Соответствующие обозначения для приемной антенны будут Р2, D2. Определим сущность понятия КНД. Предположим, что рядом расположены две антенны: направленная А и всенаправленная В. На рис. 5.5 показаны схематично диаграммы направленности обеих антенн.
Рис. 5.5. Диаграммы направленности антенн: направленной (А) и изотропной (В)
Пусть к обеим антеннам подводятся одинаковые мощности Коэффициент направленного действия (КНД) показывает, во сколько раз необходимо увеличить мощность, подводимую к изотропному излучателю, чтобы получить такую же напряженность поля в пункте приема, как создаваемую направленной антенной. КНД является безразмерной величиной. В дальнейшем покажем, что КНД измеряют в децибелах (дБ). Учитывая направленность передающей антенны, формула действующего значения напряженности поля примет вид:
Амплитудное значение напряженности поля, пришедшего в пункт приема, находится соответственно:
Мгновенное значение напряженности электрического поля, т.е. значение поля, принимаемого в данный конкретный момент времени, определяется:
где r – расстояние, Мгновенное значение напряженности электрического поля можно записать в комплексной форме:
В приведенных выше формулах (5.7 – 5.10) физические величины измеряют в международной системе измерения СИ. Для практических расчетов расстояние лучше измерять в километрах, а не метрах, мощность – в киловаттах, а не ваттах. Поэтому, выражая мощность
Для амплитудного значения напряженности электрического поля формула примет вид:
Единицы измерения входящих в формулы (5.11), (5.12) физических величин записаны в виде индексов. Передающая и приемная антенны расположены на плоской поверхности земли на расстоянии r между собой. Покажем простейшую радиотрассу в виде схемы (рис. 5.6).
Рис. 5.6. Схема простейшей радиотрассы
Необходимо определить значение мощности, поступающей на вход приемника. Очевидно, что для определения требуемой мощности необходимо знать модуль вектора Пойнтинга, пришедшего в раскрыв приемной антенны
где Тогда мощность, поступающая на вход приемного устройства, определяется:
При проектировании радиолиний удобно пользоваться понятием «потери энергии», происходящие при распространении. Потери энергии определяют формулой:
где индекс св указывает, что речь идет о потерях при распространении в свободном пространстве. Исключим влияние антенн, т.е. положим
Потери энергии выражают обычно в децибелах на основании формулы:
Таким образом, получим формулу
Из формулы (5.17) видно, что направленность антенны КНД выражают в дБ. В практических расчетах любое математическое отношение можно выразить в децибелах. Для КНД, выраженного в децибелах, следует использовать формулу:
где Рассмотрим пример. Определить величину основных потерь при распространении электромагнитной волны в свободном пространстве в случаях: а) длина волны б) длина волны Решение: для определения величины основных потерь используем формулы
а) б) Из полученных значений заключаем, что логарифмическая шкала является более удобной в использовании, т.к. имеет существенно меньшие пределы изменения значений. При распространении радиоволн в реальных условиях происходит поглощение энергии волны и другие потери. Например, в процессе распространения земной волной происходят потери энергии за счет ее частичного проникновения в толщу земной поверхности, поэтому для учета ослабления поля радиоволны в реальных условиях вводят множитель ослабления F. В этом случае расчет действующего значения напряженности поля в пункте приема производят по формуле:
где F – множитель ослабления, r – путь, проходимый волной от пункта передачи до приемного пункта. Таким образом, определить действующее значение напряженности поля на конце радиолинии можно, если будем знать значение множителя ослабления. Задача определения множителя ослабления F является главной при проектировании радиолиний. Для расчета любой трассы необходимо правильно выбрать метод расчета множителя ослабления. В дальнейшем рассмотрим некоторые методы расчета радиотрасс. Широко применяются радиоволны, распространяющиеся земной волной. Прежде чем приступить к изучению метода расчета множителя ослабления F для таких радиолиний, обратим внимание на особенности земной поверхности.
|

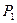 . Такой излучатель равномерно излучает энергию во все стороны пространства, а распространяющаяся волна представляет собой сферическую поверхность (рис. 5.4).
. Такой излучатель равномерно излучает энергию во все стороны пространства, а распространяющаяся волна представляет собой сферическую поверхность (рис. 5.4).
 ,
,  , (5.1)
, (5.1) ,
, 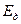 − действующее значение напряженности электрического поля,
− действующее значение напряженности электрического поля,  − действующее значение напряженности магнитного поля.
− действующее значение напряженности магнитного поля. (5.3)
(5.3) – волновое сопротивление свободного пространства:
– волновое сопротивление свободного пространства:  Ом.
Ом.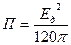 . (5.4)
. (5.4) . (5.5)
. (5.5)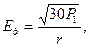 (5.6)
(5.6)
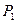 , подводимую к антенне.
, подводимую к антенне.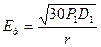 ,
,  . (5.7)
. (5.7) ,
,  ,
,  − волновое число, с – скорость света, ω; – циклическая частота,
− волновое число, с – скорость света, ω; – циклическая частота,  − КНД передающей антенны.
− КНД передающей антенны. ,
,  , расстояние r в километрах
, расстояние r в километрах  , получим напряженность поля
, получим напряженность поля  ,
,  . (5.11)
. (5.11) ,
, 
 , и учесть площадь раскрыва антенны, с помощью которого «собирается» вся приходящая энергия волны. Предварительно введем понятие эффективной площади антенны
, и учесть площадь раскрыва антенны, с помощью которого «собирается» вся приходящая энергия волны. Предварительно введем понятие эффективной площади антенны 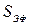 ,которая в антенно-фидерной технике определяется формулой:
,которая в антенно-фидерной технике определяется формулой: (5.13)
(5.13) − КНД приемной антенны, λ; – длина волны. Плотность потока энергии, поступающей в раскрыв антенны
− КНД приемной антенны, λ; – длина волны. Плотность потока энергии, поступающей в раскрыв антенны  , определим на основании формулы (5.1), т.е.
, определим на основании формулы (5.1), т.е. 
 ,
,  . (5.14)
. (5.14) (5.15)
(5.15)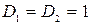 (обе антенны являются изотропными излучателями). Тогда из формулы (5.15) получим основные потери энергии, связанные только с распространением в свободном пространстве.
(обе антенны являются изотропными излучателями). Тогда из формулы (5.15) получим основные потери энергии, связанные только с распространением в свободном пространстве. (5.16)
(5.16)



 . (5.17)
. (5.17) дБ, (5.18)
дБ, (5.18) − мощность, равная одному ватту, т.е.
− мощность, равная одному ватту, т.е.  = 1Вт. Тогда отношение
= 1Вт. Тогда отношение 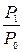 получается безразмерной величиной.
получается безразмерной величиной. м и расстояние между пунктами связи r = 10 км;
м и расстояние между пунктами связи r = 10 км; см и расстояние между пунктами связи r =
см и расстояние между пунктами связи r =  км.
км.
 Расчеты показали следующие значения основных потерь:
Расчеты показали следующие значения основных потерь: =39,3 или
=39,3 или  или
или 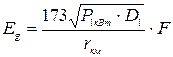 ,
, 


