Отражение и преломление плоской волны на границе раздела сред
При распространении плоской электромагнитной волны в пространстве, представляющем собой области с различными значениями параметров Коэффициентом отражения волны
Коэффициентом прохожденияволны
Если вектор Пойнтинга падающей волны перпендикулярен границе раздела, то
где Z1, Z2 – характеристическое сопротивление соответствующих сред. Характеристическое сопротивление определяется по формуле:
где
При наклонном падении направление распространения волны по отношению к границе раздела задается углом падения. Угол падения – угол между нормалью к поверхности и направлением распространения луча. Плоскость падения – это плоскость, которая содержит падающий луч и нормаль, восстановленную в точку падения. Из граничных условий следует, что углы падения
где n1, n2 – показатели преломления соответствующих сред. Электромагнитные волны характеризуются поляризацией. Различают эллиптическую, круговую и линейную поляризации. В линейной поляризации выделяют горизонтальную и вертикальную поляризацию. Вертикальная поляризация – поляризация, при которой вектор При вертикальной (параллельной) поляризации коэффициенты отражения и прохождения выражаются следующим образом (рис. 3.7).
Рис. 3.7. Падение волны с вертикальной поляризацией на границу раздела сред
В нашем случае мы должны выявить тангенциальные проекции векторов, т.е. соответственно запишем
Линии напряженности магнитного поля направлены для падающей, отраженной и преломленной волн перпендикулярно плоскости падения. Поэтому следует записать
Исходя из этого, составим на основании граничных условий систему
Известно, что напряженности электрического и магнитного полей связаны между собой через волновое сопротивление среды Z
Тогда второе уравнение системы запишем в виде
Итак, система уравнений приобрела вид
Разделим оба уравнения этой системы на амплитуду падающей волны
Система имеет два решения и две неизвестные величины. Такая система разрешима.
(3.82)
При падении плоских электромагнитных волн с параллельной поляризацией на границу раздела двух сред коэффициент отражения может обращаться в ноль. Угол падения, при котором падающая волна полностью, без отражения, проникает из одной среды в другую, называется углом Брюстера и обозначается как
или угол Брюстера определяют из формулы
Подчеркнем, что угол Брюстера при падении плоской электромагнитной волны на немагнитный диэлектрик может существовать лишь при параллельной поляризации. Если плоская электромагнитная волна падает под произвольным углом на границу раздела двух сред с потерями, то отраженную и преломленную волны следует считать неоднородными, так как плоскость равных амплитуд должна совпадать с границей раздела. Для реальных металлов угол между фазовым фронтом и плоскостью равных амплитуд мал, поэтому можно полагать, что угол преломления равен 0. Горизонтальная поляризация – поляризация, при которой вектор Пусть на границу раздела двух сред падает плоская электромагнитная волна с горизонтальной поляризацией (рис. 3.8). Вектор Пойнтинга падающей волны обозначен Для отраженной волны соответствующие векторы поля снабжены индексом «отр», для преломленной индексом – «пр». При горизонтальной (перпендикулярной) поляризации нахождение коэффициентов отражения и прохождения находят следующим образом (рис. 3.8).
Рис. 3.8. Падение волны с горизонтальной поляризацией на границу раздела сред
На границе раздела двух сред выполняются граничные условия, т.е.
Такую систему уравнений аналогичным образом можно привести к виду
Решением системы являются выражения для коэффициентов отражения и прохождения:
(3.85)
3.8. Приближенные граничные условия Щукина – Леонтовича
Данные граничные условия применимы в случае, если одна из сред является хорошим проводником. Предположим, что плоская электромагнитная волна падает под углом j из воздуха на плоскую границу раздела с хорошо проводящей средой, которая описывается комплексным показателем преломления:
Из определения понятия хорошо проводящей среды следует, что Используя граничные условия Леонтовича, необходимо определить касательную составляющую магнитного вектора
|

 и границей раздела двух сред в виде плоскости, возникают отраженные и преломленные волны. Интенсивности этих волн определяют через коэффициенты отражения и преломления.
и границей раздела двух сред в виде плоскости, возникают отраженные и преломленные волны. Интенсивности этих волн определяют через коэффициенты отражения и преломления. называется отношение комплексных значений напряженностей электрического поля отраженной волны к падающей на границе раздела и определяется формулой:
называется отношение комплексных значений напряженностей электрического поля отраженной волны к падающей на границе раздела и определяется формулой:

 . (3.77)
. (3.77) во вторую среду из первой называется отношение комплексных значений напряженностей электрического поля преломленной
во вторую среду из первой называется отношение комплексных значений напряженностей электрического поля преломленной 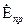 к падающей
к падающей 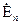 волн и определяется формулой
волн и определяется формулой
 . (3.78)
. (3.78) (3.79)
(3.79) , (3.80)
, (3.80) .
.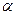 и преломления
и преломления  связаны законом Снелля:
связаны законом Снелля: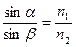 , (3.81)
, (3.81) колеблется в плоскости падения.
колеблется в плоскости падения.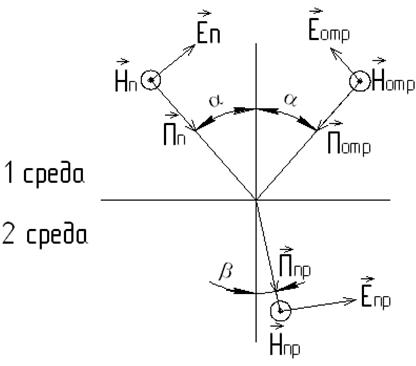

 .
. .
. .
. .
.
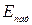 и, учитывая определения коэффициентов преломления (3.77) и прохождения (3.78), запишем систему в виде
и, учитывая определения коэффициентов преломления (3.77) и прохождения (3.78), запишем систему в виде

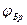
 , (3.83)
, (3.83) . (3.84)
. (3.84) . Т.к. волна имеет горизонтальную поляризацию, т.е. вектор напряженности электрического поля колеблется в плоскости, перпендикулярной плоскости падения, то он обозначен
. Т.к. волна имеет горизонтальную поляризацию, т.е. вектор напряженности электрического поля колеблется в плоскости, перпендикулярной плоскости падения, то он обозначен  и на рис. 3.8 показан в виде кружочка с крестиком (направлен от нас). Соответственно вектор напряженности магнитного поля лежит в плоскости падения волны и обозначен
и на рис. 3.8 показан в виде кружочка с крестиком (направлен от нас). Соответственно вектор напряженности магнитного поля лежит в плоскости падения волны и обозначен  . Векторы
. Векторы 




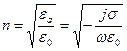 . (3.86)
. (3.86) . Применив закон Снелля, можно отметить, что угол преломления b будет очень малым. Поэтому можно считать, что преломленная волна входит внутрь хорошо проводящей среды практически по направлению нормали при любом значении угла падения.
. Применив закон Снелля, можно отметить, что угол преломления b будет очень малым. Поэтому можно считать, что преломленная волна входит внутрь хорошо проводящей среды практически по направлению нормали при любом значении угла падения. . Обычно приближенно полагают, что эта величина совпадает с аналогичной составляющей, вычисленной на поверхности идеального проводника. Ошибка, возникающая при таком приближении, будет очень мала, так как коэффициент отражения от поверхности металлов, как правило, близок к нулю.
. Обычно приближенно полагают, что эта величина совпадает с аналогичной составляющей, вычисленной на поверхности идеального проводника. Ошибка, возникающая при таком приближении, будет очень мала, так как коэффициент отражения от поверхности металлов, как правило, близок к нулю.


