Уравнения Гельмгольца
Максвелл доказал, что распространение электромагнитных процессов в пространстве с течением времени происходит в виде волны. Рассмотрим доказательство этого положения, т.е. докажем волновой характер электромагнитного поля. Запишем первые два уравнения Максвелла в комплексной форме в виде
Возьмем второе уравнение системы (3.12) и применим к нему операцию ротора к левой и правой частям. В результате получим
Обозначим
где
Учитывая закон Гаусса, т.е.
Аналогично, пользуясь симметрией уравнений Максвелла, можно получить уравнение относительно вектора
Уравнения вида (3.17, 3.18) называются уравнениями Гельмгольца. В математике доказано, что если какой-либо процесс описывается в виде уравнений Гельмгольца, то это означает, что процесс является волновым. В нашем случае делаем заключение: переменные во времени электрическое и магнитное поля неизбежно приводят к распространению в пространстве электромагнитных волн.
В координатной форме уравнение Гельмгольца (3.17) записывают в виде
где или
|
(3.12)
. (3.13)
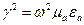, представляющую собой постоянную распространения. Таким образом, имеем
. (3.14) С другой стороны, на основе известного тождества в векторном анализе запишем
, (3.15)
является оператором Лапласа, который в декартовой системе координат выражается тождеством
. (3.16)
, уравнение (3.15) запишется в упрощенном виде
или
. (3.17)
, т.е.
. (3.18)
, (3.19)
, 
, 
– единичные векторы вдоль соответствующих осей координат,
,
, (3.20)
.
