Свойства плоских волн при распространении в непоглощающих средах
Пусть плоская электромагнитная волна распространяется вдоль оси z, тогда распространение волны описывается системой дифференциальных уравнений
где
Решение системы (3.21) имеет вид
Если волна распространяется только в одном направлении вдоль оси z, и вектор
где Если в среде отсутствуют потери, т.е. параметры среды eа, mа и Перечислим свойства плоских электромагнитных волн: 1. Для среды вводится понятие волнового сопротивления среды
где Для воздуха волновое сопротивление составляет
2. Из уравнения (3.24) видно, что магнитное и электрическое поля совпадают по фазе. Поле плоской волны представляет собой бегущую волну, которая записывается в виде
Рис. 3.4. Распространение плоской электромагнитной волны
На рис. 3.4 векторы поля 3. Вектор Пойнтинга в любой момент времени совпадает с направлением распространения волны
Модуль вектора Пойнтинга определяет плотность потока мощности и измеряется в 4. Средняя плотность потока мощности определяется по формуле:
или
где Энергия поля, заключенная в единице объема, называется плотностью энергии. Электромагнитное поле изменяется с течением времени, т.е. является переменным. Значение плотности энергии в данный момент времени называется мгновенной плотностью энергии. Для электрической
Учитывая, что Полная плотность электромагнитной энергии
5. Фазовая скорость
6. Длина волны λ; определяется формулой
где 7. Скорость перемещения энергии (групповая скорость
где Если расписать
Таким образом, получим соотношение
При распространении электромагнитной монохроматической волны в среде без потерь выполняется равенство фазовой и групповой скорости. Между фазовой и групповой скоростью существует связь, выраженная формулой
Рассмотрим пример распространения электромагнитной волны во фторопласте, имеющем параметры e =2, m=1. Пусть напряженность электрического поля соответствует
Скорость распространения волны в такой среде будет равна
Волновое сопротивление в среде из фторопласта соответствует значению
Амплитудные значения напряженности магнитного поля принимают значения
Плотность потока энергии, соответственно, равна
Длина волны на частоте
3.4. Теорема Умова – Пойнтинга
Электромагнитное поле характеризуется собственной энергией поля, причем полная энергия определяется суммой энергий электрического и магнитного полей. Пусть электромагнитное поле занимает замкнутый объем V. Тогда можно записать
Энергия электромагнитного поля, в принципе, не может оставаться постоянной величиной. Возникает вопрос: какие факторы влияют на изменение энергии? Установлено, что на изменение энергии внутри замкнутого объема влияют следующие факторы: - превращение части энергии электромагнитного поля в другие виды энергии, например, механическую; - действие внутри замкнутого объема сторонних сил, которые способны увеличивать или уменьшать энергию электромагнитного поля, заключенную в рассматриваемом объеме; - обмен энергией рассматриваемого замкнутого объема V с окружающими телами за счет процесса излучения энергии. Интенсивность излучения характеризуется вектором Пойнтинга
Рис. 3.5. Излучение энергии из объема V
Напомним, что
Переход от интеграла по поверхности Зная, что
Из формулы (3.48) видно, что левая часть выражается суммой, состоящей из трех слагаемых, каждое из которых рассмотрим в отдельности. Слагаемое Второе слагаемое Если Последнее слагаемое для линейной среды представим в виде:
Формула (3.49) выражает скорость изменения энергии электромагнитного поля, заключенного внутри объема V. После рассмотрения всех слагаемых формулу (3.48) запишем в виде:
Формула (3.50) выражает собой теорему Пойнтинга. Теорема Пойнтинга выражает баланс энергии внутри произвольной области, в которой существует электромагнитное поле.
|

 (3.21)
(3.21)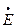 и
и 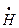 – комплексные амплитуды поля,
– комплексные амплитуды поля,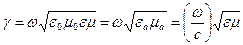 . (3.22)
. (3.22)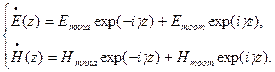 (3.23)
(3.23)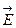 направлен вдоль оси x, то решение системы уравнений целесообразно записать в виде
направлен вдоль оси x, то решение системы уравнений целесообразно записать в виде (3.24)
(3.24) и
и 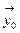 – единичные орты вдоль оси x, y.
– единичные орты вдоль оси x, y.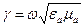 являются действительными величинами.
являются действительными величинами.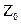
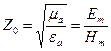 , (3.25)
, (3.25)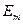 ,
, 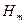 – амплитудные значения напряженностей поля. Волновое сопротивление для среды без потерь также является действительной величиной.
– амплитудные значения напряженностей поля. Волновое сопротивление для среды без потерь также является действительной величиной.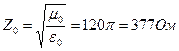 . (3.26)
. (3.26)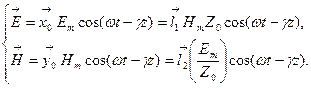 (3.27)
(3.27)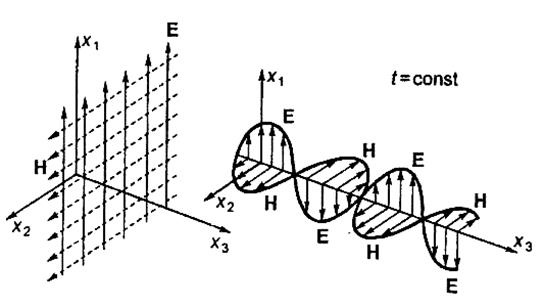
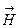 изменяются синфазно, как следует из формулы (3.27).
изменяются синфазно, как следует из формулы (3.27).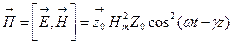 . (3.28)
. (3.28)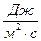 .
.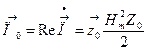 (3.29)
(3.29) , (3.30)
, (3.30)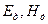 – действующие значения напряженностей поля.
– действующие значения напряженностей поля.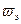 и магнитной
и магнитной 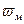 составляющих электромагнитного поля мгновенные плотности энергии соответственно равны:
составляющих электромагнитного поля мгновенные плотности энергии соответственно равны: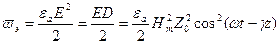 , (3.31)
, (3.31)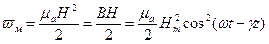 . (3.32)
. (3.32)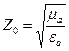 , из соотношений (3.31) и (3.32) видно, что
, из соотношений (3.31) и (3.32) видно, что 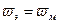 .
.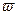 определяется выражением
определяется выражением
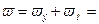
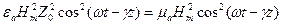 . (3.33)
. (3.33)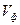 распространения электромагнитной волны определяется формулой
распространения электромагнитной волны определяется формулой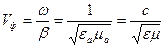 . (3.34)
. (3.34)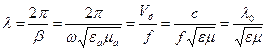 , (3.35)
, (3.35) – длина волны в вакууме (воздухе), с – скорость света в воздухе, e – относительная диэлектрическая проницаемость, m – относительная магнитная проницаемость, f – линейная частота, w – циклическая частота, V ф – фазовая скорость, b – постоянная распространения.
– длина волны в вакууме (воздухе), с – скорость света в воздухе, e – относительная диэлектрическая проницаемость, m – относительная магнитная проницаемость, f – линейная частота, w – циклическая частота, V ф – фазовая скорость, b – постоянная распространения.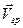 ) можно определить из формулы
) можно определить из формулы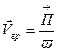 , (3.36)
, (3.36) – вектор Пойнтинга, v – плотность электромагнитной энергии.
– вектор Пойнтинга, v – плотность электромагнитной энергии. . (3.37)
. (3.37)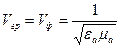 . (3.38)
. (3.38)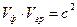 . (3.39)
. (3.39)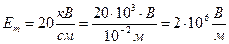 . (3.40)
. (3.40)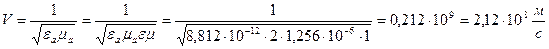 . (3.41)
. (3.41)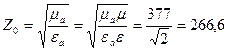 Ом. (3.42)
Ом. (3.42)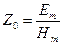 ,
, 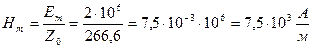 . (3.43)
. (3.43) . (3.44)
. (3.44)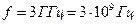 имеет значение
имеет значение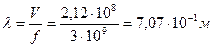 . (3.45)
. (3.45)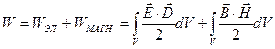 . (3.46)
. (3.46)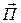 . Объем V имеет замкнутую поверхность S. Изменение энергии электромагнитного поля рассматривают как поток вектора Пойнтинга сквозь замкнутую поверхность S (рис. 3.5), т.е.
. Объем V имеет замкнутую поверхность S. Изменение энергии электромагнитного поля рассматривают как поток вектора Пойнтинга сквозь замкнутую поверхность S (рис. 3.5), т.е. 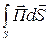 , причем возможны варианты
, причем возможны варианты 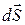 , всегда является внешней.
, всегда является внешней.
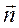
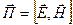 , где
, где  – это мгновенные значения напряженности поля:
– это мгновенные значения напряженности поля: (3.47)
(3.47)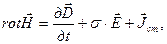
 подставим эти выражения в формулу (3.47). После преобразования получим выражение в виде:
подставим эти выражения в формулу (3.47). После преобразования получим выражение в виде: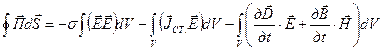 . (3.48)
. (3.48)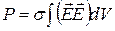 выражает мгновенную мощность потерь, обусловленную в рассматриваемом замкнутом объеме токами проводимости. Иными словами, слагаемое выражает тепловые потери энергии поля, заключенного в замкнутом объеме.
выражает мгновенную мощность потерь, обусловленную в рассматриваемом замкнутом объеме токами проводимости. Иными словами, слагаемое выражает тепловые потери энергии поля, заключенного в замкнутом объеме.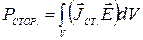 выражает работу сторонних сил, произведенную в единицу времени, т.е. мощность сторонних сил. Для такой мощности возможны значения
выражает работу сторонних сил, произведенную в единицу времени, т.е. мощность сторонних сил. Для такой мощности возможны значения 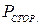 >0,
>0, 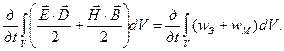 (3.49)
(3.49)
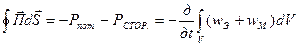 . (3.50)
. (3.50)


