Граничные условия для тангенциальных составляющих магнитного поля
Решение задачи о тангенциальных составляющих магнитного поля на границе раздела двух сред решается при помощи закона полного тока для некоторого контура, проведенного в окрестностях точки Р (рис. 2.2).
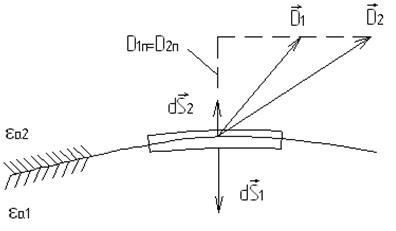
Рис. 2.2. Тангенциальные составляющие электромагнитного поля
Контур расположен перпендикулярно линии раздела двух сред. Направление обхода контура выберем против часовой стрелки. Применим к рассматриваемому контуру закон полного тока и вычислим циркуляцию вектора напряженности магнитного поля по контуру:
Необходимо рассмотреть два случая: 1. Параметры обеих сред характеризуются конечными значениями. При стремлении боковой стороны контура к нулю циркуляция вектора напряженности магнитного поля по боковым сторонам будет также стремиться к нулю. Учитывая поставленные условия о конечности параметров, имеем
Отсюда получаем соотношение
Поскольку напряженность магнитного поля выражается формулой
то можно записать граничные условия для тангенциальной составляющей вектора напряженности магнитного поля
Таким образом, при конечных значениях параметров двух сред на границе раздела этих сред тангенциальные составляющие напряженности магнитного поля будут непрерывны, а тангенциальные составляющие векторов магнитной индукции терпят разрыв. 2. Проводимость одной из граничных сред стремится к бесконечности. При бесконечно большой проводимости, например, второй среды, глубина проникновения электромагнитных волн на любой частоте равна нулю. В результате токи проводимости протекают по поверхности.
|
циркуляция по боковым сторонам 
. (2.9)
. (2.10)
.
,
. (2.11)
