Рассмотрим поведение веществ, помещенных во внешнее магнитное поле с индукцией  . В этом случае мы рассматриваем не сам заряд, а именно движущийся заряд. Таким зарядом является движущийся по круговой орбите электрон. Как известно, направленное движение заряда представляет собой электрический ток. Поэтому движение электрона по орбите следует рассматривать как электрический ток силой
. В этом случае мы рассматриваем не сам заряд, а именно движущийся заряд. Таким зарядом является движущийся по круговой орбите электрон. Как известно, направленное движение заряда представляет собой электрический ток. Поэтому движение электрона по орбите следует рассматривать как электрический ток силой  . Введем понятие элементарного магнитного диполя – это движущийся по орбите электрон, обладающий орбитальным магнитным моментом. Элементарный электрический ток характеризуется магнитным моментом
. Введем понятие элементарного магнитного диполя – это движущийся по орбите электрон, обладающий орбитальным магнитным моментом. Элементарный электрический ток характеризуется магнитным моментом  , который определяют формулой
, который определяют формулой
 , (1.66)
, (1.66)
где  – магнитный момент,
– магнитный момент,  – сила тока,
– сила тока,  – вектор элементарной площадки. На рис. 1.21 показано графическое изображение элементарного тока с вектором магнитного момента
– вектор элементарной площадки. На рис. 1.21 показано графическое изображение элементарного тока с вектором магнитного момента  .
.
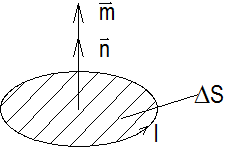
Рис. 1.21. Направление вектора элементарного магнитного момента
Магнетиками называются вещества, способные намагничиваться. Если магнетик помещен в пространство, в котором отсутствует магнитное поле, то магнитные моменты имеют хаотичную ориентацию, как показано на рис. 1.22а. Если магнетик помещен в магнитное поле с индукцией  , то под действием этого поля элементарные магнитные моменты
, то под действием этого поля элементарные магнитные моменты  ориентируются в пространстве таким образом, чтобы вектор магнитного момента был сонаправлен с вектором магнитной индукции
ориентируются в пространстве таким образом, чтобы вектор магнитного момента был сонаправлен с вектором магнитной индукции  , т.е.
, т.е.  . Упорядоченная ориентация молекулярных токов также показана на рис. 1.22б.
. Упорядоченная ориентация молекулярных токов также показана на рис. 1.22б.
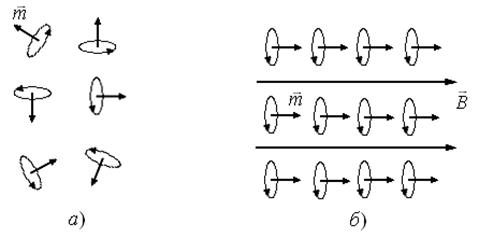
Рис. 1.22. Поведение магнетиков в магнитном поле
Описанный процесс называется намагничиванием. Иными словами, намагничивание – это процесс частичной ориентации молекул магнетика во внешнем магнитном поле.
 Намагниченность вещества характеризуется вектором намагниченности
Намагниченность вещества характеризуется вектором намагниченности  , который определяется формулой
, который определяется формулой
 , (1.67)
, (1.67)
где  – вектор намагниченности вещества,
– вектор намагниченности вещества,  – концентрация молекул,
– концентрация молекул,  – элементарный магнитный момент.
– элементарный магнитный момент.
Экспериментально установлено, что у большинства веществ при не слишком больших магнитных полях существует связь между вектором намагниченности и напряженностью внешнего действующего магнитного поля. Такую связь выражают линейной зависимостью в виде формулы

 , (1.68)
, (1.68)
где  – намагниченность,
– намагниченность,  – напряженность поля,
– напряженность поля,  – магнитная восприимчивость вещества.
– магнитная восприимчивость вещества.
Установлено, что магнитные свойства вещества можно описать, если вектор магнитной индукции  представить в виде:
представить в виде:
 , (1.69)
, (1.69)
где  – магнитная постоянная,
– магнитная постоянная,  – напряженность магнитного поля,
– напряженность магнитного поля,  – намагниченность вещества. Учитывая формулу (1.68), можно формулу (1.69) записать в виде
– намагниченность вещества. Учитывая формулу (1.68), можно формулу (1.69) записать в виде
 . (1.70)
. (1.70)
Введем обозначение
 , (1.71)
, (1.71)
где величина  называется абсолютной магнитной проницаемостью вещества.
называется абсолютной магнитной проницаемостью вещества.
Уравнение (1.70) с учетом формулы (1.71) принимает более простой вид
 , (1.72)
, (1.72)
где  – абсолютная магнитная проницаемость вещества.
– абсолютная магнитная проницаемость вещества.
 Если среда является вакуумом, то намагниченность
Если среда является вакуумом, то намагниченность 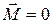 и связь между
и связь между  и
и  принимает более простой вид
принимает более простой вид
 . (1.73)
. (1.73)
Для практических расчетов часто используют относительную магнитную проницаемость, которая определяется отношением

 . (1.74)
. (1.74)
Все магнетики (вещества) в зависимости от значения относительной магнитной проницаемости делят на три класса:
- диамагнетики, если  ;
;
- парамагнетики, если  ;
;
- ферромагнетики, если  .
.
Для большинства веществ относительная магнитная проницаемость близка к единице. В таблице 1.2 приведены значения относительной магнитной проницаемости для некоторых веществ.
Таблица 1.2
Относительная диэлектрическая проницаемость
| Вещество
| Относительная диэлектрическая проницаемость 
|
| Вода
Кислород
Медь
Серебро
Алюминий
| 0,9999905
1,00000191
0,99999044
0,9999736
1,0000222
|
Формула связи между  и
и  в виде
в виде  указывает на линейный характер связи. Отметим, что для ферромагнетиков такая связь имеет нелинейный характер.
указывает на линейный характер связи. Отметим, что для ферромагнетиков такая связь имеет нелинейный характер.
В ферромагнетиках существуют отдельные микроскопические области (домены), имеющие размеры порядка  . Внутри домена все элементарные магнитные моменты параллельны между собой. Поэтому каждый домен ферромагнетика обладает собственным магнитным моментом, величина которого зависит от структуры вещества и не зависит от внешнего поля. Если внешнее магнитное поле отсутствует, то магнитные моменты доменов ориентированы хаотично, а суммарный магнитный момент равен нулю. Если ферромагнетик находится во внешнем магнитном поле, то происходит ориентация магнитных моментов по направлению внешнего магнитного поля.
. Внутри домена все элементарные магнитные моменты параллельны между собой. Поэтому каждый домен ферромагнетика обладает собственным магнитным моментом, величина которого зависит от структуры вещества и не зависит от внешнего поля. Если внешнее магнитное поле отсутствует, то магнитные моменты доменов ориентированы хаотично, а суммарный магнитный момент равен нулю. Если ферромагнетик находится во внешнем магнитном поле, то происходит ориентация магнитных моментов по направлению внешнего магнитного поля.
Уравнения в виде  ,
,  называют материальными уравнениями или уравнениями состояния среды. Материальные уравнения справедливы для широкого класса материальных сред, но применимость этих уравнений имеет ограничения. Например, на высоких частотах векторы поляризации
называют материальными уравнениями или уравнениями состояния среды. Материальные уравнения справедливы для широкого класса материальных сред, но применимость этих уравнений имеет ограничения. Например, на высоких частотах векторы поляризации  и намагничивания
и намагничивания  не успевают мгновенно следовать за изменением воздействующего внешнего поля. В этом случае наблюдается явление запаздывания. В результате параметры среды становятся зависимыми от частоты действующего электромагнитного поля. Такое явление носит название частотной дисперсии среды.
не успевают мгновенно следовать за изменением воздействующего внешнего поля. В этом случае наблюдается явление запаздывания. В результате параметры среды становятся зависимыми от частоты действующего электромагнитного поля. Такое явление носит название частотной дисперсии среды.
Основная особенность материальных уравнений заключается в их линейном характере. При дальнейшем изучении будем полагать, что в рассматриваемых средах выполняется линейность материальных уравнений. Помимо линейных, существуют нелинейные среды. Например, нелинейность среды проявляется при больших значениях напряженности полей. Так, электрическая нелинейность характерна для электромагнитных полей, создаваемых мощными лазерами. Упомянутые выше ферромагнетики проявляют магнитную нелинейность, а сегнетодиэлектрики – электрическую нелинейность среды при достаточно умеренных значениях напряженностей полей.

 . В этом случае мы рассматриваем не сам заряд, а именно движущийся заряд. Таким зарядом является движущийся по круговой орбите электрон. Как известно, направленное движение заряда представляет собой электрический ток. Поэтому движение электрона по орбите следует рассматривать как электрический ток силой
. В этом случае мы рассматриваем не сам заряд, а именно движущийся заряд. Таким зарядом является движущийся по круговой орбите электрон. Как известно, направленное движение заряда представляет собой электрический ток. Поэтому движение электрона по орбите следует рассматривать как электрический ток силой  . Введем понятие элементарного магнитного диполя – это движущийся по орбите электрон, обладающий орбитальным магнитным моментом. Элементарный электрический ток характеризуется магнитным моментом
. Введем понятие элементарного магнитного диполя – это движущийся по орбите электрон, обладающий орбитальным магнитным моментом. Элементарный электрический ток характеризуется магнитным моментом  , который определяют формулой
, который определяют формулой , (1.66)
, (1.66) – вектор элементарной площадки. На рис. 1.21 показано графическое изображение элементарного тока с вектором магнитного момента
– вектор элементарной площадки. На рис. 1.21 показано графическое изображение элементарного тока с вектором магнитного момента 
 . Упорядоченная ориентация молекулярных токов также показана на рис. 1.22б.
. Упорядоченная ориентация молекулярных токов также показана на рис. 1.22б.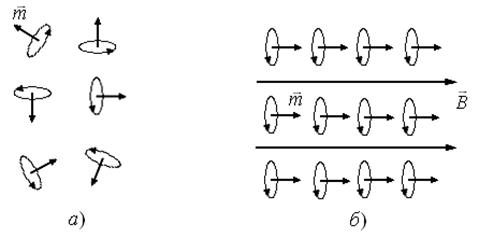
 Намагниченность вещества характеризуется вектором намагниченности
Намагниченность вещества характеризуется вектором намагниченности  , который определяется формулой
, который определяется формулой , (1.67)
, (1.67) – концентрация молекул,
– концентрация молекул,  – элементарный магнитный момент.
– элементарный магнитный момент.
 , (1.68)
, (1.68) – напряженность поля,
– напряженность поля,  – магнитная восприимчивость вещества.
– магнитная восприимчивость вещества. представить в виде:
представить в виде: , (1.69)
, (1.69) – магнитная постоянная,
– магнитная постоянная,  . (1.70)
. (1.70) , (1.71)
, (1.71) называется абсолютной магнитной проницаемостью вещества.
называется абсолютной магнитной проницаемостью вещества. , (1.72)
, (1.72)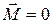 и связь между
и связь между  и
и  . (1.73)
. (1.73)
 . (1.74)
. (1.74) ;
; ;
; .
.
 указывает на линейный характер связи. Отметим, что для ферромагнетиков такая связь имеет нелинейный характер.
указывает на линейный характер связи. Отметим, что для ферромагнетиков такая связь имеет нелинейный характер. . Внутри домена все элементарные магнитные моменты параллельны между собой. Поэтому каждый домен ферромагнетика обладает собственным магнитным моментом, величина которого зависит от структуры вещества и не зависит от внешнего поля. Если внешнее магнитное поле отсутствует, то магнитные моменты доменов ориентированы хаотично, а суммарный магнитный момент равен нулю. Если ферромагнетик находится во внешнем магнитном поле, то происходит ориентация магнитных моментов по направлению внешнего магнитного поля.
. Внутри домена все элементарные магнитные моменты параллельны между собой. Поэтому каждый домен ферромагнетика обладает собственным магнитным моментом, величина которого зависит от структуры вещества и не зависит от внешнего поля. Если внешнее магнитное поле отсутствует, то магнитные моменты доменов ориентированы хаотично, а суммарный магнитный момент равен нулю. Если ферромагнетик находится во внешнем магнитном поле, то происходит ориентация магнитных моментов по направлению внешнего магнитного поля. ,
,  и намагничивания
и намагничивания 


