Запаздывающие потенциалы
Запишем уравнения Максвелла в комплексной форме:
Пусть в однородной среде существуют сторонние токи. Попробуем преобразовать уравнения Максвелла для такой среды и получить более простое уравнение, описывающее электромагнитное поле в ней. Возьмем уравнение
Возьмем второе уравнение системы Максвелла (3.51) и выполним преобразования:
т.е.
Формула (3.53) выражает второе уравнение Максвелла через векторный потенциал
или
В электростатике, как известно, выполняется соотношение
где Выражение в скобках (3.54) по аналогии с формулой (3.55) запишем в виде
или
где Ф – скалярный электродинамический потенциал. Возьмем первое уравнение Максвелла и запишем его с помощью электродинамических потенциалов:
или
или
В векторной алгебре доказано тождество
Используя тождество (3.58), можно первое уравнение Максвелла, записанное в виде (3.57), представить в виде
или
Приведем подобные
Умножим левую и правую части на множитель (–1):
Поскольку
Выражение (3.60) называется лоренцевой калибровкой. Если w=0, то получим кулонову калибровку С учетом калибровок уравнение (3.59) можно записать как:
Уравнение (3.61) выражает собой неоднородное волновое уравнение для векторного электродинамического потенциала. Аналогичным путем, исходя из третьего уравнения Максвелла
где V – объем, занимаемый сторонними токами, r – текущее расстояние от каждого элемента объема источника до точки М. Решения для векторного электродинамического потенциала (3.63), (3.64) называются интегралом Кирхгофа для запаздывающих потенциалов. Множитель
Этот множитель соответствует конечной скорости распространения волны от источника, причем
Рис. 3.6. Излучение энергии точечным источником
В момент времени t векторный потенциал Из формулы (3.64) видно, что векторный электродинамический потенциал параллелен (сонаправлен) плотности тока сторонних сил; его амплитуда убывает по закону Учитывая
Полученные соотношения определяют электромагнитное поле в пространстве, созданном заданным распределением сторонних токов.
|

 (3.51)
(3.51) . Зная, что характеристики
. Зная, что характеристики  и
и  связаны между собой
связаны между собой  , можно записать
, можно записать  Учтем, что напряженность магнитного поля можно выразить с помощью векторного электродинамического потенциала
Учтем, что напряженность магнитного поля можно выразить с помощью векторного электродинамического потенциала  , который вводится соотношением
, который вводится соотношением  , тогда
, тогда . (3.52)
. (3.52)
 (3.53)
(3.53)
 (3.54)
(3.54)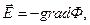 (3.55)
(3.55)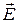 – вектор напряженности поля, Ф – скалярный электростатический потенциал. Знак минус указывает, что вектор
– вектор напряженности поля, Ф – скалярный электростатический потенциал. Знак минус указывает, что вектор 
 (3.56)
(3.56)

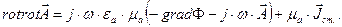 (3.57)
(3.57) (3.58)
(3.58)


 (3.59)
(3.59)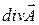 можно задать произвольным образом, можно положить, что
можно задать произвольным образом, можно положить, что
 . (3.60)
. (3.60)
 . (3.61)
. (3.61)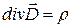 , можно получить неоднородное уравнение для скалярного электродинамического потенциала в виде:
, можно получить неоднородное уравнение для скалярного электродинамического потенциала в виде: (3.62)
(3.62) Полученные неоднородные уравнения для электродинамических потенциалов имеют свои решения в виде
Полученные неоднородные уравнения для электродинамических потенциалов имеют свои решения в виде , (3.63)
, (3.63) – объемная плотность заряда, γ; – постоянная распространения, r – текущее расстояние от каждого элемента объема источника до точки М.
– объемная плотность заряда, γ; – постоянная распространения, r – текущее расстояние от каждого элемента объема источника до точки М. , (3.64)
, (3.64) с учетом
с учетом  выразим в виде
выразим в виде
 Т.к. скорость распространения волны является конечной величиной, то воздействие источника, порождающего волны, до произвольной точки М доходит с запаздыванием во времени. Значение времени запаздывания определяется по формуле:
Т.к. скорость распространения волны является конечной величиной, то воздействие источника, порождающего волны, до произвольной точки М доходит с запаздыванием во времени. Значение времени запаздывания определяется по формуле:  На рис. 3.6 показан точечный источник U, который излучает сферические волны, распространяющиеся со скоростью v в окружающем однородном пространстве, а также произвольная точка М, расположенная на расстоянии r, до которой доходит волна.
На рис. 3.6 показан точечный источник U, который излучает сферические волны, распространяющиеся со скоростью v в окружающем однородном пространстве, а также произвольная точка М, расположенная на расстоянии r, до которой доходит волна.
 в точке М является функцией токов, протекающих в источнике U в более раннее время
в точке М является функцией токов, протекающих в источнике U в более раннее время 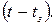 Иными словами,
Иными словами,  ; на больших расстояниях по сравнению с размерами излучателя волна имеет сферический фронт волны.
; на больших расстояниях по сравнению с размерами излучателя волна имеет сферический фронт волны. и первое уравнение Максвелла, определим напряженность электрического поля:
и первое уравнение Максвелла, определим напряженность электрического поля: (3.65)
(3.65)


