OpenGL ES для новичков
8.2.1. Метод безпосереднього інтегрування Метод інтегрування, при якому даний інтеграл шляхом тотожних перетворень підінтегральної функції (або виразу) і застосування властивостей невизначеного інтеграла зводиться до одного або декількох табличних інтегралів, називається безпосереднім інтегруванням. При зведенні даного інтеграла до табличного часто використовуються наступні перетворення диференціала (операція «приведення під знак диференціала»):
Взагалі, Приклади: 1) 2) 3)
4) 5)
6)
7) 8)
9)
10) 11) 12)
13)
Як бачимо, обчислення інтегралів іноді вимагає деякої винахідливості, так би мовити, «індивідуального підходу до кожної підінтегральної функції». Відповідні навички отримуються в результаті значного числа вправ. 8.2.2. Метод інтегрування підстановкою (заміна змінної) Інтегрування методом підстановки полягає у введенні нової змінної інтегрування (тобто підстановкою). При цьому заданий інтеграл приводиться до нового інтеграла, який є табличним або таким, що зводиться до нього (у разі «вдалої підстановки»). Загальних методів підбору підстановок не існує. Уміння правильно визначити підстановку отримується практикою. Нехай потрібно обчислити інтеграл Тоді
Формула (2.1) також називається формулою заміни змінних в невизначеному інтегралі. Після знаходження інтеграла правої частини цієї рівності слід перейти від нової змінної інтеграції Іноді доцільно підбирати підстановку у вигляді Приклад 1. Знайти m Покладемо Приклад 2. Знайти m Нехай
Приклад 3. Отримати формулу mПозначимо Звідси
Отже
Приклад 4. Знайти m Нехай
Приклад 5. Знайти m Позначимо
Тут використовується формула 16 таблиці основних інтегралів. l 8.2.3. Метод інтегрування частинами Нехай
Отримана формула називається формулою інтегрування частинами. Вона дає можливість звести обчислення інтеграла Інтегрування частинами полягає в тому, що підінтегральний вираз заданого інтеграла представляється яким-небудь чином у вигляді добутку двох співмножників Вкажемо деякі типи інтегралів, які зручно обчислювати методом інтегрування частинами. 1. Інтеграл вигляду 2. Інтеграли вигляду 3. Інтеграли вигляду Приклад 6. Знайти m Нехай
Приклад 7. Знайти m Нехай
Приклад 8. Знайти m Нехай
Для обчислення інтеграла
Тому (див. (2.2)) Приклад 9. Знайти m Нехай
8.3. ІНТЕГРУВАННЯ РАЦІОНАЛЬНИХ ФУНКЦІЙ 8.3.1. Поняття про раціональні функції Многочлен (деякі відомості довідкового характеру) Функція вигляду
де Число Коренем многочлена (3.1) називається таке значення Теоремa 8.3.1. Якщо
де Виникає питання: чи всякий многочлен має корінь? Позитивну відповідь на це питання дає наступне твердження. Теорема 8.3.2. (основна теорема алгебри). Всякий многочлен Доведення цієї теореми ми не приводимо. Користуючись основною теоремою алгебри, доведемо теорему про розкладання многочлена на лінійні множники. Теорема 8.3.3. Всякий многочлен
де q Розглянемо многочлен (3.1). По теоремі 8.3.2 він має корінь. Позначимо його через Тоді Продовжуючи цей процес, отримаємо у результаті:
Множники Приклад 1. Розкласти многочлен m Многочлен Приклад 2. Представити вираз m Легко перевірити, що Якщо в розкладанні многочлена (3.3) який-небудь корінь зустрівся Розкладання многочлена (3.3) можна записати у вигляді
якщо корінь При цьому Наприклад, розкладання
можна записати так:
Користуючись теоремою 31.3, можна довести наступні твердження. Теорема 8.3.4. Якщо многочлен Теорема 8.3.5. Якщо два многочлени тотожно рівні один одному, то коефіцієнти одного многочлена рівні відповідним коефіцієнтам іншого. Наприклад, якщо, Теорема 8.3.6. Якщо многочлен В розкладанні многочлена (3.3) комплексні корені входять спряженими парами. Перемноживши лінійні множники
отримаємо тричлен другого степеня з дійсними коефіцієнтами Таким чином, добуток лінійних множників, відповідних зв'язаним кореням, можна замінити квадратним тричленом з дійсними коефіцієнтами. З урахуванням вищевикладеного справедливий наступний факт. Теорема 8.3.7. Всякий многочлен з дійсними коефіцієнтами розкладається на лінійні і квадратні множники з дійсними коефіцієнтами, тобто многочлен
При цьому Приклади розкладань (3.5): 1) 2) 3) Дробово-раціональна функція Дробово-раціональною функцією (або раціональним дробом) називається функція, рівна відношенню двох многочленів, тобто Раціональний дріб називається правильним, якщо степінь чисельника менше степеня знаменника, тобто Всякий неправильний раціональний дріб Наприклад, _ х4 –5х +9| х–2 х4–2х3 |х3 +2x2 +4x+3 _ 2х3 –5х + 9 2х3–4х2 _4х2 – 5х + 9 4х2 – 8х _ 3х + 9 3х – 6 15. Отримаємо частку
Правильні раціональні дроби вигляду (I). (II). (III). (IV). Теорема 8.3.8. Всякий правильний раціональний дріб
де Пояснимо формулювання теореми на наступних прикладах: 1) 2) 3) Для знаходження невизначених коефіцієнтів Суть методу така: 1. В правій частині рівності (3.6) зведемо до спільного знаменника 2. Оскільки в отриманій тотожності знаменники рівні, то тотожно рівні і чисельники, тобто
3. Прирівнюючи коефіцієнти при однакових степенях Приклад 3. Подати дріб m Згідно теореми 31.8 маємо:
Звідси слідує
Прирівнюючи коефіцієнти при
Розв’язуючи систему, знаходимо, що
Для знаходження невизначених коефіцієнтів застосовують також метод окремих значень аргументу: після отримання тотожності (3.7) аргументу Приклад 4. Подати дріб m Маємо: Покладемо
8.3.2. Інтегрування найпростіших раціональних дробів Знайдемо інтеграли від найпростіших раціональних дробів. 1. 2. 3. Розглянемо інтеграл Виділивши в знаменнику повний квадрат, отримаємо:
причому
тобто, повертаючись до змінної
Приклад 5. Знайти m
4. Обчислення інтеграла вигляду Даний інтеграл підстановкою Перший інтеграл легко обчислюється:
Обчислимо другий інтеграл:
До останнього інтеграла застосуємо інтегрування частинами. Покладемо
Підставляючи знайдений інтеграл в рівність (3.8), отримаємо
Отримана формула дає можливість знайти інтеграл Приклад 6. Знайти інтеграл m Тут
8.3.3. Інтегрування раціональних дробів Розглянутий в пунктах 1-3 матеріал дозволяє сформулювати загальне правило інтеграції раціональних дробів. 1. Якщо дріб неправильний, то подати його у вигляді суми многочлена і правильного дробу (див. пункт 2); 2. Розклавши знаменник правильного раціонального дробу на множники, подати його у вигляді суми найпростіших раціональних дробів; 3. Проінтегрувати многочлен і отриману суму найпростіших дробів. Приклад 7. Знайти інтеграл m Під знаком інтеграла неправильний дріб; виділимо його цілу частину шляхом ділення чисельника на знаменник:
_ x5 +2x3 +4x+4| x4 +2x3 +2x2 х5+2x4 +2x3 |x–2 _–2x4 +4x+4 –2x4–4x3–4x2 4x3+4x2+4x+4 (остача). Отримаємо: Розкладемо правильний раціональний дріб на найпростіші дроби:
Звідси слідує, що
Знаходимо:
Інтегруємо отриману рівність:
Позначимо
Отже
Відзначимо, що будь-яка раціональна функція інтегрується в елементарних функціях. 8.4. ІНТЕГРУВАННЯ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ 8.4.1. Універсальна тригонометрична підстановка Розглянемо деякі випадки знаходження інтеграла від тригонометричних функцій. Функцію із змінними Обчислення невизначених інтегралів типу Дійсно Тому де На практиці застосовують і інші, більш прості підстановки, залежно від властивостей (і вигляду) підінтегральної функції. Зокрема, зручні наступні правила: 1) якщо функція 2) якщо функція 3) якщо функція Приклад 1. Знайти інтеграл m Зробимо універсальну підстановку Приклад 2. Знайти інтеграл m Оскільки
Тому 8.4.2. Інтеграли виду Для знаходження таких інтегралів використовуються наступні прийоми: 1) підстановка 2) підстановка 3) формули пониження порядку: 4) підстановка Приклад 3. Знайти інтеграл m Застосуємо підстановку
Приклад 4. Знайти інтеграл m
Приклад 5. Знайти інтеграл m Тут
8.4.3. Використання тригонометричних перетворень Інтеграли типу
Приклад 6. Знайти інтеграл m 8.5. ІНТЕГРУВАННЯ ІРРАЦІОНАЛЬНИХ ФУНКЦІЙ 8.5.1. Квадратичні ірраціональності Розглянемо деякі типи інтегралів, що містять ірраціональні функції. Інтеграли типу
і зробити підстановку Приклад 1. Знайти інтеграли m Оскільки Зробимо підстановку
Приклад 2. Знайти інтеграл m Оскільки
Інтеграли типу
де Всі невизначені коефіцієнти знаходяться з тотожності, отриманої диференціюванням обох частин рівності (5.1):
Приклад 3. Знайти інтеграл m По формулі (5.1) маємо:
Диференціюючи цю рівність, отримаємо:
Звідси
8.5.2. Дробово-лінійна підстановка Інтеграли виду Дійсно, з підстановки Приклад 4. Знайти інтеграл m Найменше спільне кратне знаменників дробів
Приклад 5. Вказати підстановку для знаходження інтегралів: m Для 8.5.3. Тригонометрична підстановка Інтеграли типу Приклад 6. Знайти інтеграл m Покладемо
8.5.4. Інтеграли виду
|

 ,
,  – число
– число ,
,  – число
– число ,
, ,
, ,
,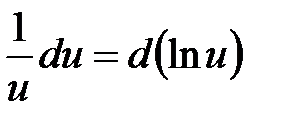 ,
, .
.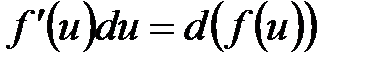 , ця формула дуже часто використовується при обчисленні інтегралів.
, ця формула дуже часто використовується при обчисленні інтегралів.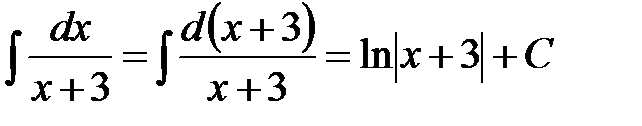 (формула 2 таблиці інтегралів);
(формула 2 таблиці інтегралів); (формула 1);
(формула 1);
 (формули 10 і 1);
(формули 10 і 1);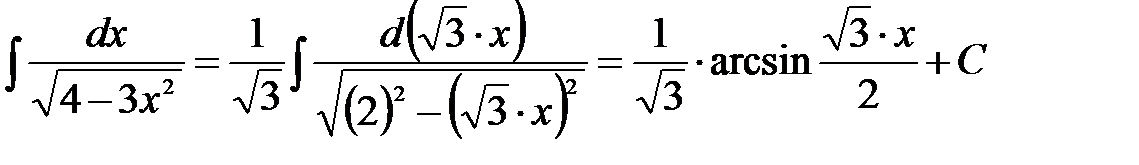 (формула 13);
(формула 13);
 (формули 1 і 6);
(формули 1 і 6);
 ;
; (виведення формули 7);
(виведення формули 7);


 (виведення формули 11);
(виведення формули 11);

 (формула 1);
(формула 1);
 (формула 1);
(формула 1);
 (формула 14);
(формула 14);

 (формули 1,9,3);
(формули 1,9,3);


 .
. . Зробимо підстановку
. Зробимо підстановку  , де
, де 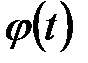 – функція, що має неперервну похідну.
– функція, що має неперервну похідну. і на підставі властивості інваріантності формули інтеграції невизначеного інтеграла отримуємо формулу інтегрування підстановкою
і на підставі властивості інваріантності формули інтеграції невизначеного інтеграла отримуємо формулу інтегрування підстановкою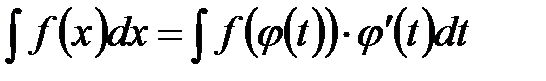 (2.1)
(2.1) назад до змінної
назад до змінної 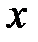 .
. , тоді
, тоді  , де
, де 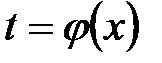 . Іншими словами, формулу (2.1) можна застосовувати справа наліво.
. Іншими словами, формулу (2.1) можна застосовувати справа наліво. .
. , тоді
, тоді  . Отже
. Отже 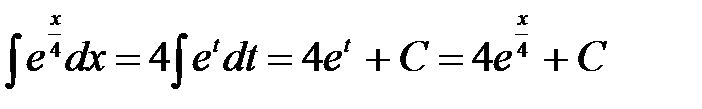 . l
. l .
. , тоді
, тоді  ,
,  . Тому
. Тому 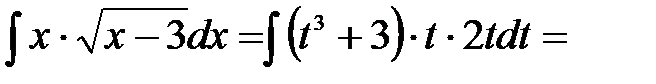

 .l
.l .
. (підстановка Ейлера). Тоді
(підстановка Ейлера). Тоді  , тобто
, тобто  .
. .
.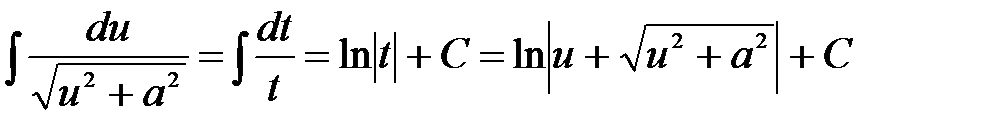 . l
. l .
. . Тоді
. Тоді  ,
,  . Маємо:
. Маємо:
 . l
. l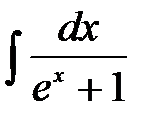 .
.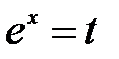 . Тоді
. Тоді  ,
, 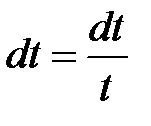 . Отже
. Отже

 .
. і
і  - функція, що має неперервні похідні. Тоді
- функція, що має неперервні похідні. Тоді  . Проінтегрувавши цю рівність, отримаємо
. Проінтегрувавши цю рівність, отримаємо або
або 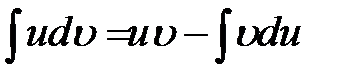
 до обчислення інтеграла
до обчислення інтеграла  , який може виявитися істотно простішим за початковий.
, який може виявитися істотно простішим за початковий. і
і  (це, як правило, можна здійснити декількома способами); потім, після знаходження
(це, як правило, можна здійснити декількома способами); потім, після знаходження  і
і 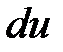 використовується формула інтегрування частинами. Іноді цю формулу потрібно використовувати кілька разів.
використовується формула інтегрування частинами. Іноді цю формулу потрібно використовувати кілька разів.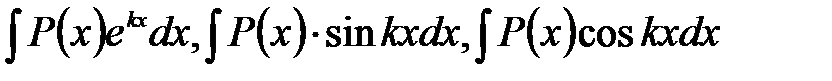 ,
, 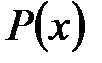 - многочлен,
- многочлен,  – число. Зручно покласти
– число. Зручно покласти  , а за
, а за 
 . Зручно покласти
. Зручно покласти  , а за
, а за  позначити решту співмножників.
позначити решту співмножників.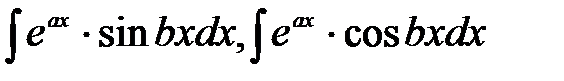 , де
, де  і
і  – числа. За
– числа. За  можна прийняти функцію
можна прийняти функцію  .
.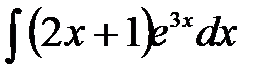 .
. (можна покласти
(можна покласти  ). Отже, по формулі інтегрування частинами:
). Отже, по формулі інтегрування частинами:
 . l
. l .
.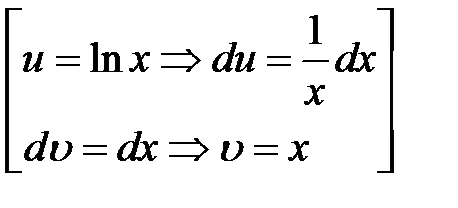 . Тому
. Тому .l
.l .
. . Тому
. Тому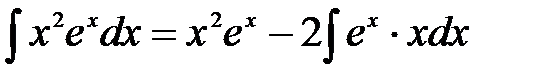 . (2.2)
. (2.2) знову застосуємо метод інтегрування частинами:
знову застосуємо метод інтегрування частинами: 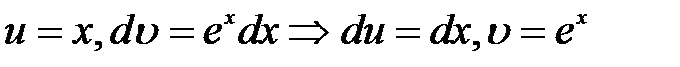 . Значить
. Значить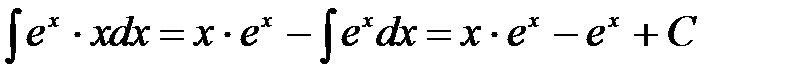 . (2.3)
. (2.3) . l
. l .
. . Тому
. Тому
 .l
.l (3.1)
(3.1) — натуральне число,
— натуральне число,  — постійні коефіцієнти, називається многочленом (або цілою раціональною функцією).
— постійні коефіцієнти, називається многочленом (або цілою раціональною функцією).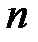 називається степенем многочлена.
називається степенем многочлена. (взагалі кажучи, комплексне) змінної
(взагалі кажучи, комплексне) змінної  , при якому многочлен перетворюється в нуль, тобто
, при якому многочлен перетворюється в нуль, тобто  .
. є коренем многочлена
є коренем многочлена  , то многочлен ділиться без остачі на
, то многочлен ділиться без остачі на  тобто
тобто (3.2)
(3.2) — многочлен степеня
— многочлен степеня 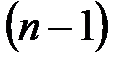 .
. -го степеня
-го степеня  має принаймні один корінь, дійсний або комплексний.
має принаймні один корінь, дійсний або комплексний.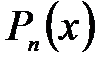 можна подати у вигляді
можна подати у вигляді (3.3)
(3.3) — корені многочлена,
— корені многочлена,  — коефіцієнт многочлена при
— коефіцієнт многочлена при  .
. . Тоді має місце співвідношення (3.2). А оскільки
. Тоді має місце співвідношення (3.2). А оскільки  — також многочлен, то він має корінь. Позначимо його через
— також многочлен, то він має корінь. Позначимо його через  .
. , де
, де  — многочлен
— многочлен  -го степеня. Отже,
-го степеня. Отже,  .
. . n
. n в рівності (3.3) називаються лінійними множниками.
в рівності (3.3) називаються лінійними множниками. на множники.
на множники. перетворюється в нуль при
перетворюється в нуль при  . Отже,
. Отже,  . l
. l у вигляді добутку лінійних множників.
у вигляді добутку лінійних множників. l
l раз, то він називається коренем кратності
раз, то він називається коренем кратності 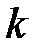 . У випадку
. У випадку 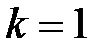 (тобто корінь зустрівся один раз) корінь називається простим.
(тобто корінь зустрівся один раз) корінь називається простим. , (3.4)
, (3.4)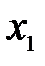 має кратність
має кратність  , корінь
, корінь  – кратність
– кратність  і так далі.
і так далі. , а
, а  – число різних коренів.
– число різних коренів.
 .
.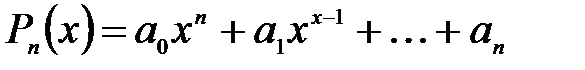 тотожно рівний нулю, то всі його коефіцієнти рівні нулю.
тотожно рівний нулю, то всі його коефіцієнти рівні нулю.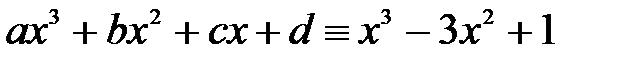 , то
, то  .
. з дійсними коефіцієнтами має комплексний корінь
з дійсними коефіцієнтами має комплексний корінь  , то він має і зв'язаний корінь
, то він має і зв'язаний корінь  .
. ,
, . Насправді,
. Насправді, 
 де
де  .
. можна подати у вигляді
можна подати у вигляді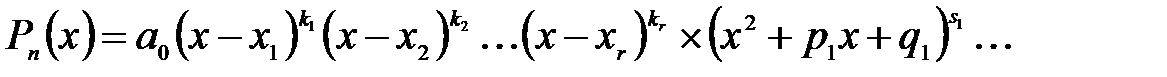
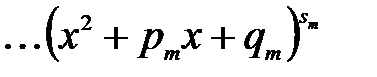 . (3.5)
. (3.5) всі квадратні тричлени не мають речовинних коренів.
всі квадратні тричлени не мають речовинних коренів.

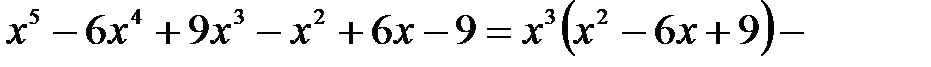


 , де
, де  - многочлен степеня
- многочлен степеня  , а
, а  - многочлен степеня
- многочлен степеня  .
. ; в протилежному випадку (якщо
; в протилежному випадку (якщо  ) раціональний дріб називається неправильним.
) раціональний дріб називається неправильним. можна, шляхом ділення чисельника на знаменник, подати у вигляді суми многочлена
можна, шляхом ділення чисельника на знаменник, подати у вигляді суми многочлена  і правильного раціонального дробу
і правильного раціонального дробу 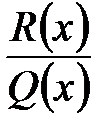 , тобто
, тобто  .
. – неправильний раціональний дріб. Розділимо чисельник на знаменник в стовпчик:
– неправильний раціональний дріб. Розділимо чисельник на знаменник в стовпчик: і залишок
і залишок  . Отже,
. Отже, .
.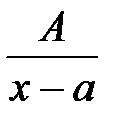 ;
;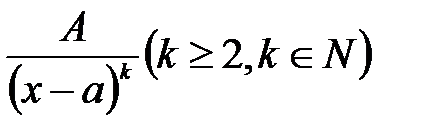 ;
;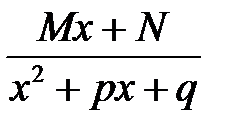 (корені знаменника комплексні, тобто
(корені знаменника комплексні, тобто 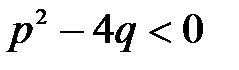 );
); (
( , корені знаменника комплексні), де
, корені знаменника комплексні), де  - дійсні числа, називаються найпростішими раціональними дробами I, II, III і IV типів.
- дійсні числа, називаються найпростішими раціональними дробами I, II, III і IV типів.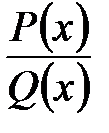 , знаменник якого розкладений на множники
, знаменник якого розкладений на множники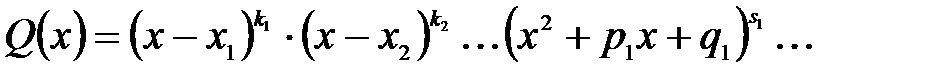
 , можна подати (і притому єдиним чином) у вигляді наступної суми найпростіших дробів:
, можна подати (і притому єдиним чином) у вигляді наступної суми найпростіших дробів: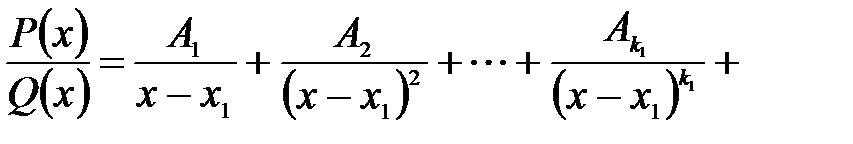



 , (3.6)
, (3.6) – деякі дійсні коефіцієнти.
– деякі дійсні коефіцієнти. ;
; ;
;
 .
. в рівності (3.6) можна застосувати метод порівняння коефіцієнтів.
в рівності (3.6) можна застосувати метод порівняння коефіцієнтів.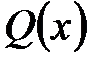 ; в результаті отримаємо тотожність
; в результаті отримаємо тотожність  , де
, де  – многочлен з невизначеними коефіцієнтами.
– многочлен з невизначеними коефіцієнтами. . (3.7)
. (3.7) (по теоремі 31.5 про тотожність многочленів) в обох частинах тотожності (3.7), отримаємо систему лінійних рівнянь, з якої і визначимо шукані коефіцієнти
(по теоремі 31.5 про тотожність многочленів) в обох частинах тотожності (3.7), отримаємо систему лінійних рівнянь, з якої і визначимо шукані коефіцієнти 
 у вигляді суми найпростіших дробів.
у вигляді суми найпростіших дробів. , тобто
, тобто .
.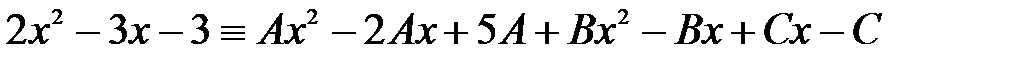 , тобто
, тобто .
.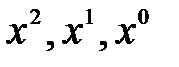 , отримаємо
, отримаємо
 . Отже,
. Отже, . l
. l надають конкретні значення стільки раз, скільки невизначених коефіцієнтів (звичайно вважають за
надають конкретні значення стільки раз, скільки невизначених коефіцієнтів (звичайно вважають за  ).
). у вигляді суми найпростіших дробів.
у вигляді суми найпростіших дробів. . Звідси слідує
. Звідси слідує 
 , тоді
, тоді 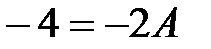 , тобто
, тобто 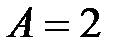 ; покладемо
; покладемо  , тоді
, тоді 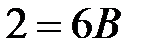 , тобто
, тобто  ; покладемо
; покладемо 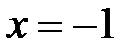 , тоді
, тоді  , тобто
, тобто  . Отже
. Отже .l
.l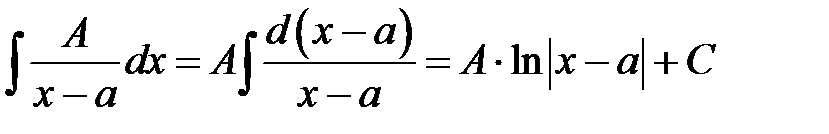 (формула (2) таблиці інтегралів);
(формула (2) таблиці інтегралів); (формула (1));
(формула (1)); .
. ,
, . Зробимо підстановку
. Зробимо підстановку 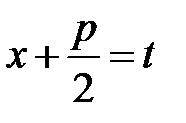 . Тоді
. Тоді  ,
,  . Покладемо
. Покладемо  . Отже, використовуючи формули (2) і (15) таблиці інтегралів, отримуємо:
. Отже, використовуючи формули (2) і (15) таблиці інтегралів, отримуємо: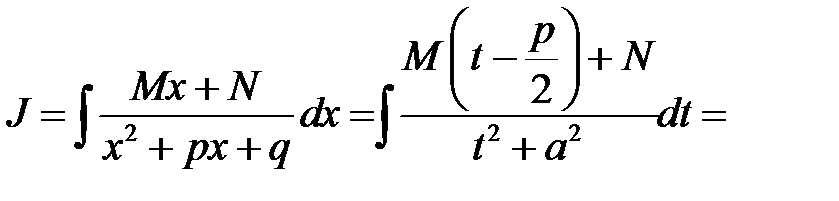

 ,
,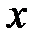
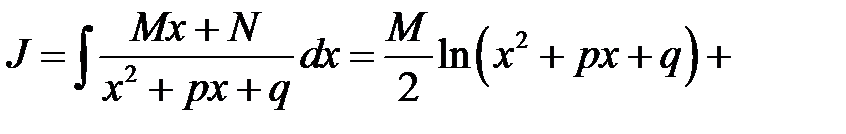
 .
. .
. . Зробимо підстановку
. Зробимо підстановку 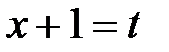 . Тоді
. Тоді 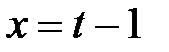 ,
, 

 . l
. l .
.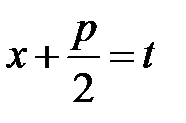 зводиться до суми двох інтегралів:
зводиться до суми двох інтегралів:  ,
,  .
.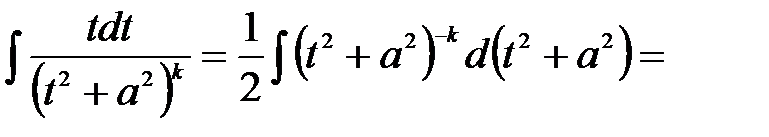
 .
.
 . (3.8)
. (3.8)
 , тоді
, тоді

 , тобто
, тобто .
.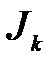 для будь-якого натурального числа
для будь-якого натурального числа  .
. .
. до
до 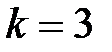 . Оскільки
. Оскільки  , то
, то
 ,
,
 . l
. l .
.
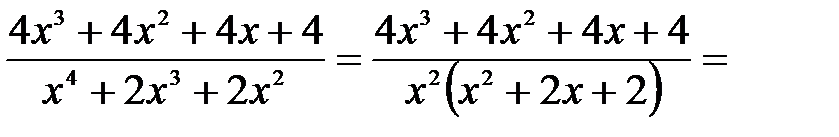
 ,
,
 , тобто
, тобто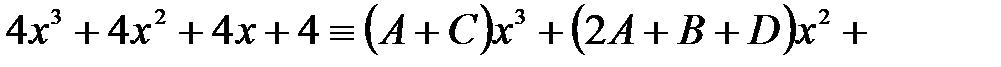
 .
.
 . Отже
. Отже , і
, і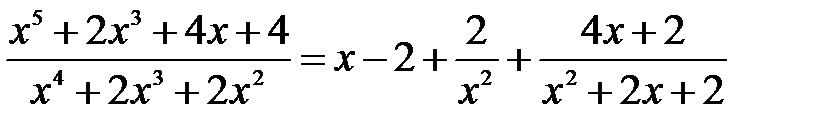 .
.
 .
. , тоді
, тоді  і
і  . Таким чином
. Таким чином

 .
.
 . l
. l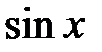 і
і  , над якими виконуються раціональні дії (додавання, віднімання, множення і ділення) прийнято позначати
, над якими виконуються раціональні дії (додавання, віднімання, множення і ділення) прийнято позначати  , де
, де  – знак раціональної функції.
– знак раціональної функції.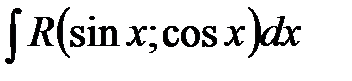 зводиться до обчислення інтегралів від раціональної функції підстановкою
зводиться до обчислення інтегралів від раціональної функції підстановкою  , яка називається універсальною.
, яка називається універсальною.
 .
.
 - раціональна функція від
- раціональна функція від  . Звичайно, цей спосіб досить громіздкий, зате він завжди приводить до результату.
. Звичайно, цей спосіб досить громіздкий, зате він завжди приводить до результату.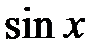 , тобто
, тобто 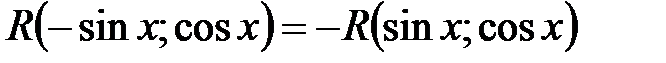 , то підстановку
, то підстановку  раціоналізує інтеграл;
раціоналізує інтеграл; , тобто
, тобто  , то виконується підстановка
, то виконується підстановка  ;
; і
і  , тобто
, тобто  , то інтеграл раціоналізується підстановкою
, то інтеграл раціоналізується підстановкою  . Така ж підстановка застосовується, якщо інтеграл має вигляд
. Така ж підстановка застосовується, якщо інтеграл має вигляд  .
.
 . Тоді,
. Тоді, 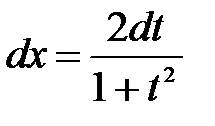 . Отже
. Отже 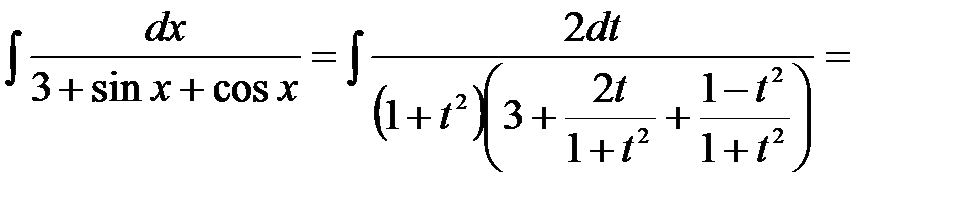
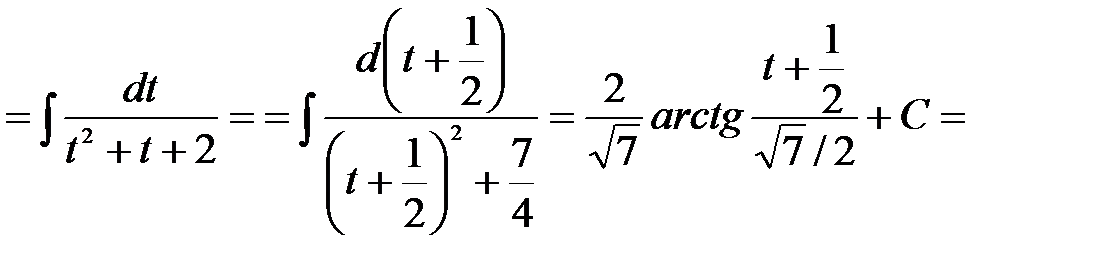
 . l
. l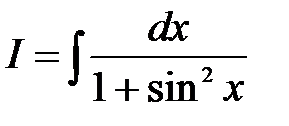 .
.
 , то вважаємо
, то вважаємо 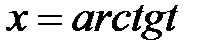 ,
,  і
і 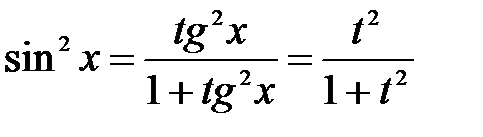 .
.
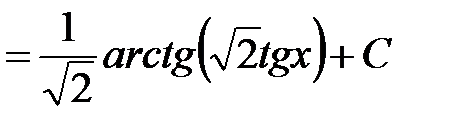 .l
.l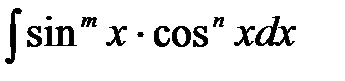
 – ціле додатне непарне число;
– ціле додатне непарне число; , якщо
, якщо  – ціле додатне непарне число;
– ціле додатне непарне число;

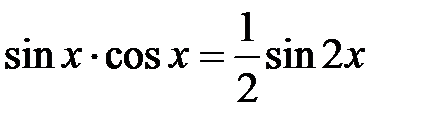 , якщо
, якщо 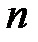 - цілі невід’ємні парні числа;
- цілі невід’ємні парні числа; , якщо
, якщо  – є парне від’ємне ціле число.
– є парне від’ємне ціле число. .
. ,
,  і
і 

 . l
. l .
.

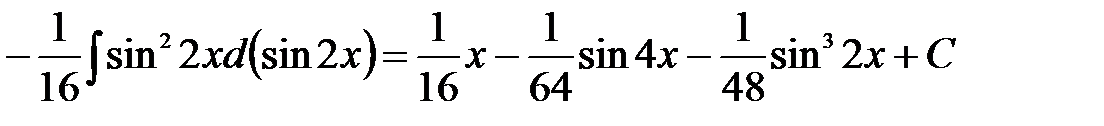 .l
.l .
. . Позначимо
. Позначимо  . Тоді
. Тоді 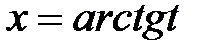 ,
,  і
і
 . l
. l ,
,  ,
,  обчислюються за допомогою відомих тригонометричних формул:
обчислюються за допомогою відомих тригонометричних формул: ,
, ,
,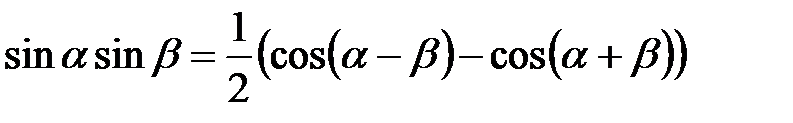 .
.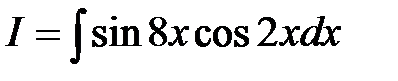 .
.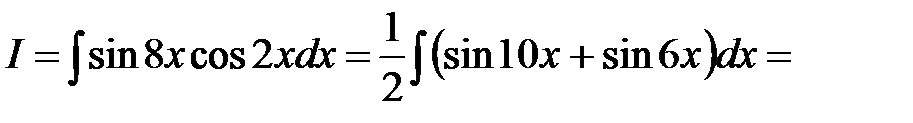
 . l
. l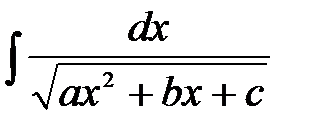 ,
, 
 називають невизначеними інтегралами від квадратичних ірраціональностей. Їх можна знайти таким чином: під радикалом виділити повний квадрат
називають невизначеними інтегралами від квадратичних ірраціональностей. Їх можна знайти таким чином: під радикалом виділити повний квадрат
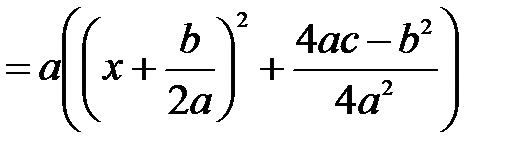
 . При цьому перші два інтеграли приводяться до табличних, а третій – до суми двох табличних інтегралів.
. При цьому перші два інтеграли приводяться до табличних, а третій – до суми двох табличних інтегралів. .
. , то
, то  .
. ,
,  ,
,  . Тоді
. Тоді
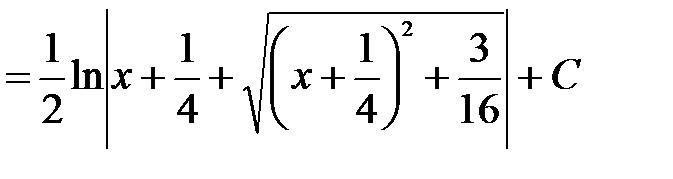 . l
. l .
. , то підстановка має вигляд
, то підстановка має вигляд  ,
,  ,
,  . Тоді
. Тоді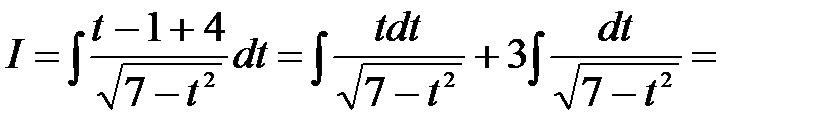


 . l
. l , де
, де  - многочлен степеня
- многочлен степеня  можна обчислювати, користуючись формулою
можна обчислювати, користуючись формулою
 (5.1)
(5.1) - многочлен степеня
- многочлен степеня  з невизначеними коефіцієнтами,
з невизначеними коефіцієнтами,  – також невизначений коефіцієнт.
– також невизначений коефіцієнт.
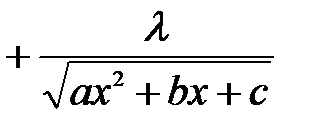 , після чого необхідно прирівняти коефіцієнти при однакових степенях невідомої
, після чого необхідно прирівняти коефіцієнти при однакових степенях невідомої  .
.

 .
.
 , тобто
, тобто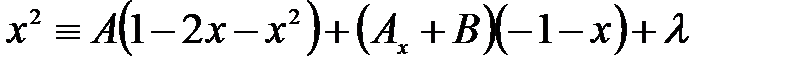 ,
, . Порівнюємо коефіцієнти при однакових степенях
. Порівнюємо коефіцієнти при однакових степенях  :
: , при
, при 
 при
при 
 при
при 


 . Отже
. Отже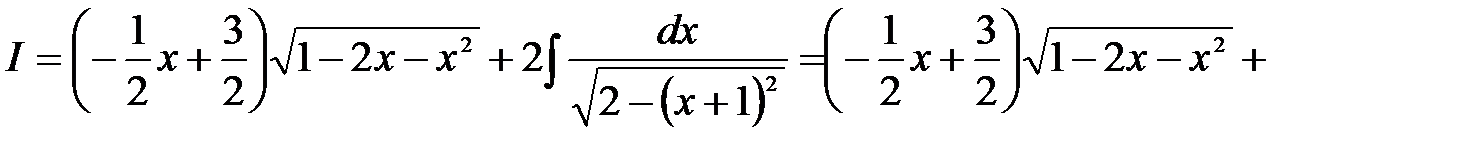
 . l
. l , де
, де  - дійсні числа,
- дійсні числа,  – натуральні числа, зводяться до інтегралів від раціональної функції шляхом підстановки
– натуральні числа, зводяться до інтегралів від раціональної функції шляхом підстановки 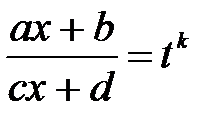 , де
, де  – найменше спільне кратне знаменників дробів
– найменше спільне кратне знаменників дробів  .
. виходить, що
виходить, що  і
і  , тобто
, тобто 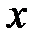 і
і  виражаються через раціональні функції від
виражаються через раціональні функції від 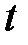 . При цьому і кожний степінь дробу
. При цьому і кожний степінь дробу  виражається через раціональну функцію від
виражається через раціональну функцію від  .
. .
. і
і 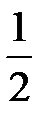 є 6. Тому вважаємо
є 6. Тому вважаємо  ,
,  ,
,  ,
,  . Отже
. Отже

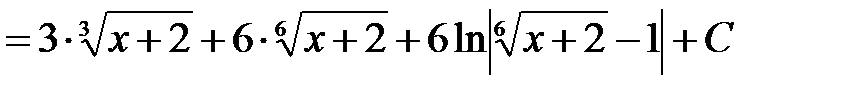 . l
. l підстановка
підстановка  , для
, для  підстановка
підстановка  . l
. l зводяться до інтегралів від функцій, раціонально залежних від тригонометричних функцій, за допомогою наступних тригонометричних підстановок:
зводяться до інтегралів від функцій, раціонально залежних від тригонометричних функцій, за допомогою наступних тригонометричних підстановок: 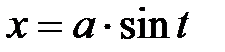 для першого інтеграла;
для першого інтеграла; 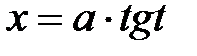 для другого інтеграла;
для другого інтеграла;  для третього інтеграла.
для третього інтеграла. .
. ,
,  ,
,  . Тоді
. Тоді
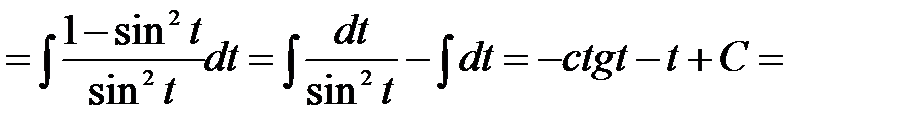

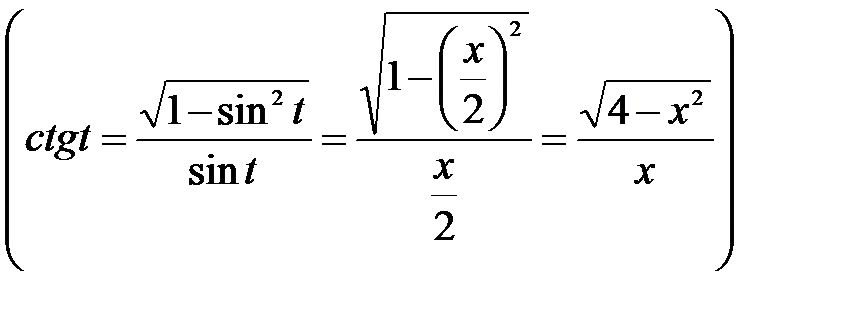 . l
. l



