Гальваномагнитный эффект Холла
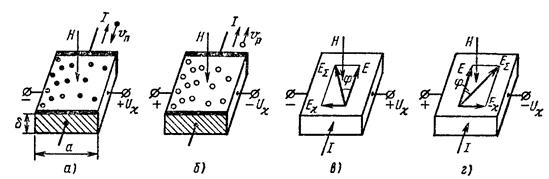
Предположим, что в пластинке полупроводника, находящейся в магнитном поле, идет ток, обусловленный движением только электронов (рис.4.14, а).
Рис.4.14. Возникновение э.д.с. Холла в полупроводнике с электропроводностью; n- типа (а, в) и p- типа (б, г)
Тогда сила Лоренца будет смещать движущиеся электроны к левой грани пластинки полупроводника. Направление смещения определяется направлением силы Лоренца, т. е. векторным произведением
с учетом знака носителей, или правилом левой руки, относящимся к техническому направлению тока. В результате смещения движущихся электронов между боковыми гранями пластинки полупроводника возникает э.д.с. Холла. В полупроводнике с электропроводностью р -типа при том же техническом направлении тока вектор скорости дырок направлен противоположно вектору скорости электронов, знак носителей заряда также другой. Поэтому сила Лоренца (4.7) действует на дырки в ту же сторону, смещая их также к левой грани пластинки полупроводника (рис.4.14, б). Полярность э.д.с. Холла при этом получается другой. Накопление носителей заряда у боковой грани пластинки полупроводника прекратится, когда сила Лоренца уравновесится силой холловского электрического поля. При перпендикулярном направлении напряженности магнитного поля к поверхности пластинки полупроводника условием такого динамического равновесия будет равенство:
Считая холловское электрическое поле однородным и учитывая геометрические размеры пластинки полупроводника, можно записать для э.д.с. Холла, т. е. для поперечной разности потенциалов между боковыми гранями пластинки полупроводника с электропроводностью p -типа:
Значение скорости дырок можно определить из формулы для тока:
Тогда
где Х = 1 /(qp) — коэффициент Холла для полупроводника с электропроводностью р -типа. Выражение (4.11) получено в предположении, что скорости у всех носителей заряда одинаковые, в действительности носители заряда в полупроводнике распределены по скоростям. Это распределение зависит от преобладающего механизма рассеяния носителей в конкретном полупроводнике. Поэтому более точное значение коэффициента Холла отличается от имеющегося в выражении (4.11) множителем А:
Величина множителя А находится в диапазоне от 1 до 2 и зависит от механизма рассеяния носителей заряда. Так, для вырожденного полупроводника А = 1, для полупроводника с преобладающим рассеянием носителей на тепловых колебаниях кристаллической решетки А = 1,18, для полупроводника с преобладающим рассеянием на ионизированных примесях А = 1,93. Для полупроводника с электропроводностью n -типа полярность э.д.с. Холла противоположна. Поэтому коэффициент Холла для такого полупроводника имеет другой знак:
В полупроводниках с приблизительно равными концентрациями электронов и дырок (например, в собственных полупроводниках) расчет коэффициента Холла получается более сложным:
После возникновения холловской напряженности электрического поля и установления динамического равновесия между силой Лоренца и силой холловского электрического поля все носители заряда, имеющие скорость V, будут двигаться по прямолинейным траекториям в соответствии с направлением внешнего электрического поля Е (рис. 4.14, в и г). При этом направление вектора суммарного электрического поля
отличается от технического направления вектора тока на некоторый угол φ (рис.4.14, в и г), который называют углом Холла. Величину угла Холла определяют по формуле
Холловская напряженность электрического поля в полупроводнике с электропроводностью p -типа, с учетом (4.11),
Напряженность в пластинке полупроводника от внешнего источника питания.
Поэтому
Очевидно, что для полупроводниковой пластинки с электропроводностью n -типа получится аналогичное соотношение между углом Холла, подвижностью электронов и величиной магнитной индукции. При малых магнитных полях и, следовательно, при малых углах Холла
или
С учетом конечной длины пластины l, подводимая мощность определяется равенством:
С учетом максимально допустимой температуры пластины, максимально допустимый ток
где S — площадь поверхности пластины (верх, низ и 2 боковые грани); β — коэффициент теплоотдачи; Δ Т — разность температур между максимально допустимой и температурой окружающей среды. Если пренебречь площадью боковых граней и считать, что S = 2аl, максимально допустимый ток через пластину составит:
Максимальная э.д.с. Холла при заданной индукции магнитного поля возникает в пластине при прохождении через нее максимально допустимого тока и составляет:
С учетом (4.12), (4.20) для проводника р-типа:
э.д.с. Холла определяется как подвижностью, так и концентрацией носителей.
|

 (4.7)
(4.7) (4.8)
(4.8) (4.9)
(4.9) (4.10)
(4.10)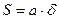 - площадь поперечного сечения пластины;
- площадь поперечного сечения пластины; - ширина пластинки;
- ширина пластинки; - толщина пластинки.
- толщина пластинки.
 (4.11)
(4.11) (4.12)
(4.12) (4.12.а)
(4.12.а) (4.13)
(4.13)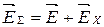 (4.14)
(4.14) (4.15)
(4.15) (4.16)
(4.16) (4.17)
(4.17)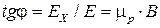 (4.18)
(4.18) (4.18.а)
(4.18.а)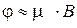 (4.19)
(4.19) (4.20)
(4.20) (4.21)
(4.21) (4.22)
(4.22) (4.22)
(4.22) (4.23)
(4.23)


