Магнитное поле прямолинейного токаТок I течёт по бесконечному прямолинейному проводнику. Вычислим индукцию магнитного поля этого тока на расстоянии l от проводника (рис. 8.6.).
Рис. 8.6. Элемент тока
Вектор В скалярной форме это уравнение можно записать так:
Для отыскания полного поля в точке А нужно просуммировать вклады всех элементов данного тока, то есть, рассмотреть интеграл:
Как следует из рисунка:
Используя эти данные в (8.6), получим:
Теперь при сложении этих вкладов, то есть, при интегрировании, будет меняться только угол a в пределах от 0 до p:
Вектор магнитной индукции поля прямолинейного тока пропорционален величине тока I и обратно пропорционален расстоянию b от проводника до рассматриваемой точки. Магнитное поле, также как и электростатическое, принято представлять графически магнитными силовыми линиями. Как и прежде, это, в общем случае, кривая, касательные к любой точке которой совпадают по направлению с векторами магнитной индукции в данных точках (рис. 8.7.).
Рис. 8.7. Густота магнитных силовых линий равна значению индукции в данной области пространства. «Густота» — это число силовых линий, проходящих через единичную поверхность, ориентированную перпендикулярно магнитному полю. Поле прямолинейного тока обладает цилиндрической симметрией. Его силовые линии — окружности с центром на оси тока (рис. 8.8.).
Рис. 8.8.
|
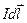создаёт в рассматриваемой точке магнитное поле:
.
направлен перпендикулярно плоскости рисунка от нас (правило буравчика).
. (8.6)
.
, 
.
.
. (8.7)
