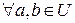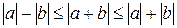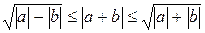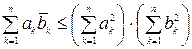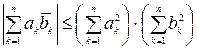Задание {{ 140 }} ТЗ № 140

⇐ Предыдущая 7 8 9 10 11 12 13 14 1516

Отметьте правильный ответ

В неравенстве Коши-Буняковского в унитарном пространстве знак равенства достигается только тогда, когда векторы х и у:

£ совпадают

£ линейно независимы

R пропорциональны

£ одинаковой длины

Следствия из неравенства Коши-Буняковского для унитарного пространство

Задание {{ 141 }} ТЗ № 141

Отметьте правильный ответ

Из неравенства Коши-Буняковского для унитарного пространства Сⁿ следует, что для любых комплексных чисел а₁,…,а_n и b₁,…,b_n:

Задание {{ 142 }} ТЗ № 142

Отметьте правильный ответ

Из неравенства Коши-Буняковского для унитарного пространства U следует, что

Задание {{ 143 }} ТЗ № 143

Отметьте правильный ответ

Из неравенства Коши-Буняковского для унитарного пространства U следует, что

Задание {{ 144 }} ТЗ № 144

Отметьте правильный ответ

Задание {{ 145 }} ТЗ № 145

Отметьте правильный ответ

Из неравенства Коши-Буняковского для унитарного пространства C₂[a,b] всех непрерывных на отрезке [a,b] функций вещественной переменной с комплексными значениями следует, что:

⇐ Предыдущая 7 8 9 10 11 12 13 14 1516

Дата добавления: 2015-10-19; просмотров: 488. Нарушение авторских прав; Мы поможем в написании вашей работы!

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...

Определение трудоемкости работ и затрат машинного времени На основании ведомости объемов работ по объекту и норм времени ГЭСН составляется ведомость подсчёта трудоёмкости, затрат машинного времени, потребности в конструкциях, изделиях и материалах (табл...

Гидравлический расчёт трубопроводов Пример 3.4. Вентиляционная труба d=0,1м (100 мм) имеет длину l=100 м. Определить давление, которое должен развивать вентилятор, если расход воздуха, подаваемый по трубе, . Давление на выходе . Местных сопротивлений по пути не имеется. Температура...

Огоньки» в основной период В основной период смены могут проводиться три вида «огоньков»: «огонек-анализ», тематический «огонек» и «конфликтный» огонек...

Тактика действий нарядов полиции по предупреждению и пресечению правонарушений при проведении массовых мероприятий К особенностям проведения массовых мероприятий и факторам, влияющим на охрану общественного порядка и обеспечение общественной безопасности, можно отнести значительное количество субъектов, принимающих участие в их подготовке и проведении...

Тактические действия нарядов полиции по предупреждению и пресечению групповых нарушений общественного порядка и массовых беспорядков В целях предупреждения разрастания групповых нарушений общественного порядка (далееГНОП) в массовые беспорядки подразделения (наряды) полиции осуществляют следующие мероприятия...

Механизм действия гормонов а) Цитозольный механизм действия гормонов. По цитозольному механизму действуют гормоны 1 группы...

Studopedia.info - Студопедия - 2014-2026 год . (0.009 сек.) русская версия | украинская версия