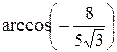Задание {{ 50 }} ТЗ № 50
Отметьте правильный ответ Периметр параллелограмма, натянутого на векторы
£
R 8
£
£
Угол между векторами в евклидовом пространстве Задание {{ 51 }} ТЗ № 51 Отметьте правильный ответ Угол φ между ненулевыми векторами евклидова пространства при умножении одного из этих векторов на положительное число λ:
R не меняется
£ меняется
£ становится равным π-φ
£ становится равным π+φ
Задание {{ 52 }} ТЗ № 52 Отметьте правильный ответ Угол φ между ненулевыми векторами евклидова пространства при умножении одного из этих векторов на отрицательное число:
£ меняется на -φ
£ не меняется
R становится равным π-φ
£ становится равным π+φ
Задание {{ 53 }} ТЗ № 53 Отметьте правильный ответ Угол φ между ненулевыми векторами евклидова пространства при умножении обоих векторов на отрицательные числа:
£ меняется на -φ
£ меняется на π-φ
R не меняется
£ меняется на π+φ
Задание {{ 54 }} ТЗ № 54 Отметьте правильный ответ В евклидовом пространстве R4 угол между векторами
£ 90
£
R
£
Задание {{ 55 }} ТЗ № 55 Отметьте правильный ответ В евклидовом пространстве R4 наибольший из углов между диагоналями параллелограмма, натянутого на векторы
R
£
£
£
|
пространства R4, равен:
равен:
равен:
