Пусть даны две прямые и .Угол
Равенство Примеры 1. Написать канонические и параметрическое уравнения прямой, проходящей через точку а) Из условия параллельности двух прямых за направляющий вектор искомой прямой возьмем вектор в) Полагая 2. Даны вершины треугольника Используем уравнение прямой, проходящей через две точки, и напишем уравнения соответствующих сторон
Тогда используя формулу 3. Написать уравнение прямой, проходящей через точку Направляющим вектором искомой прямой будет вектор, перпендикулярный векторам
Теперь можем написать каноническое уравнение искомой прямой
Плоскость в пространстве Уравнение плоскости, проходящей через заданную точку
Общее уравнение плоскости
|
между двумя прямыми будет определяться как угол между их направляющими векторами 
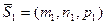и тогда
.
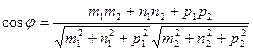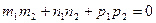будет условием перпендикулярности, а соотношение 
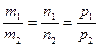будет условием параллельности двух прямых в пространстве.
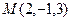, параллельно прямой 
.
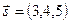, тогда каноническое уравнение параллельной прямой будет иметь вид: 
.
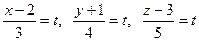, получим параметрическое уравнение параллельной прямой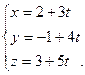 
. Найти уравнения сторон 
, 
и угол между ними.
, 
.
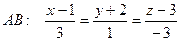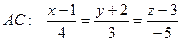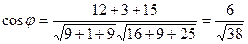, а угол между прямыми 
.
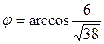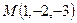перпендикулярно векторам 
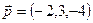и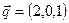 
.
= 
.
.
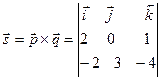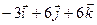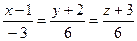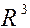
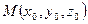и имеющей заданный вектор нормали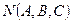 
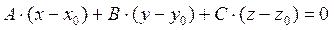. (19)
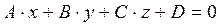(20)
