Прямая линия на плоскости
Смешанное произведение трех векторов численно равно по абсолютной величине объему параллелепипеда, построенного на векторах Если три вектора
Примеры 1. Найти смешанное произведение трех векторов
2. Вычислить объем пирамиды с вершинами: Найдем векторы Вычислим их смешанное произведение 3.Установить, лежат ли четыре точки Найдем три вектора Вычислим их смешанное произведение
Прямая линия на плоскости Уравнение прямой с угловым коэффициентом
Если 1) 2) Замечание. Уравнение Угол между двумя прямыми
Рис. 1 Из полученной формулы следует: 1. Условие параллельности двух прямых; 2. Условие перпендикулярности двух прямых; Уравнение прямой, проходящей через заданную точку
Уравнение пучка прямых
|
как на сторонах.
, 
, 
лежат в одной плоскости, то их смешанное произведение равно нулю, т.е.
= 0, что и будет условием компланарности трех векторов.
.
.
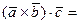
, что численно равно объему параллелепипеда,построенного на этих векторах как на сторонах. А объем пирамиды составляет шестую часть объема параллелепипеда, таким образом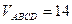 
.
в одной плоскости.
, т.е. данные векторы компланарны и, следовательно, четыре точки лежат в одной плоскости.
, 
, где 
- угол наклона прямой к оси ОХ.
, то прямая 
проходит через начало координат;
, то прямая 
совпадает с осью ОХ.
.
и 
.
. Угол между прямыми 
(рис. 1).
, Y 
. 
Х
.
.
с заданным угловым коэффициентом 
.
