Исследование общего уравнения плоскости
1) D = 0, плоскость проходит через О, т.е. через начало координат. 2) С = 0, плоскость параллельна оси ОZ. 2') B = 0, плоскость параллельна оси OY. 2") А= 0, плоскость параллельна оси OX. 3) С = D = 0, плоскость проходит через ось OZ. 3') B = D = 0, плоскость проходит через ось OY. 3'') A = D = 0, плоскость проходит через ось OX. 4) 4') параллельной плоскости OXZ и отстоящей от нее на расстоянии 4'') параллельной плоскости OYZ и отстоящей от нее на расстоянии 5) A = B = D = 0, z = 0 уравнение плоскости OXY. 5') A = C = D = 0, y = 0 уравнение плоскости OXZ. 5'') B = C = D = 0, x = 0 уравнение плоскости OYZ. Уравнение плоскости, проходящей через три заданные точки
Угол между двух плоскостей Пусть даны две плоскости
Исходя из полученной формулы, получим условие перпендикулярности двух плоскостей, а именно, Соотношение Угол между прямой и плоскостью
Прямая и плоскость будут перпендикулярны, если векторы Прямая и плоскость будут параллельны, если векторы
|
, уравнение плоскости, параллельной плоскости OXY и отстоящей от нее на расстоянии 
.
,уравнение плоскости,
.
, уравнение плоскости,
.
.
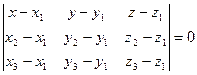и 
. Угол 
между двумя плоскостями -это угол между нормалями к этим плоскостям, т.е. между векторами 
и 
. Тогда
.
.
дает условие параллельности двух плоскостей.
.
и 
- коллинеарные, т.е. если выполняется соотношение 
.
.
