 .
.
Примеры
1. Найти плоскость, проходящую через точку 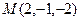 , параллельно плоскости
, параллельно плоскости  .
.
Для данной плоскости вектор нормали  . Используя условие параллельности двух плоскостей, напишем уравнение искомой плоскости:
. Используя условие параллельности двух плоскостей, напишем уравнение искомой плоскости:
 , отсюда
, отсюда  .
.
2. Составить уравнение плоскости, проходящей через точки 
Воспользуемся уравнением  , получим определитель
, получим определитель
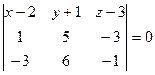 , затем – общее уравнение плоскости
, затем – общее уравнение плоскости 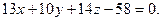
3. Составить уравнение плоскости, проходящей через точку  и прямую
и прямую  .
.
Данная прямая проходит через точку 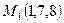 с направляющим вектором
с направляющим вектором 
 . Составим вектор
. Составим вектор  . Вектор нормали
. Вектор нормали 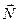 искомой плоскости должен быть перпендикулярен векторам
искомой плоскости должен быть перпендикулярен векторам 
 и
и  , т.е.
, т.е. 
 . Тогда, используя уравнение плоскости, проходящей через заданную точку с заданным вектором нормали, получим
. Тогда, используя уравнение плоскости, проходящей через заданную точку с заданным вектором нормали, получим  , отсюда получаем общее уравнение плоскости
, отсюда получаем общее уравнение плоскости  .
.
4. Найти уравнение плоскости, проходящей через точку 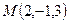 перпендикулярно плоскостям
перпендикулярно плоскостям  .
.
Векторы нормали заданных плоскостей соответственно равны  . Вектор нормали искомой плоскости должен быть перпендикулярен этим двум векторам, т.е.
. Вектор нормали искомой плоскости должен быть перпендикулярен этим двум векторам, т.е.
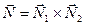

 . Тогда используя уравнение плоскости, проходящей через заданную точку с заданным вектором нормали получим
. Тогда используя уравнение плоскости, проходящей через заданную точку с заданным вектором нормали получим  ,
,  отсюда получаем общее уравнение плоскости
отсюда получаем общее уравнение плоскости 
5. Найти угол между плоскостями 
Векторы нормали заданных плоскостей соответственно равны  . Тогда используя формулу
. Тогда используя формулу  , получим
, получим  , т.е. плоскости перпендикулярны.
, т.е. плоскости перпендикулярны.
6. Доказать, что прямые  ,
,  пересекаются.
пересекаются.
Используем условие принадлежности двух прямых плоскости
 , получим определитель
, получим определитель  0. Следовательно, эти прямые пересекаются.
0. Следовательно, эти прямые пересекаются.
7. Найти точку пересечения прямой 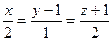 с плоскостью
с плоскостью 
Запишем параметрическое уравнение прямой  .
.
Подставим полученные  в уравнение плоскости, получим
в уравнение плоскости, получим
 , тогда
, тогда 
 . Подставляя полученное значение в параметрическое уравнение прямой, найдем координаты пересечения прямой и плоскости
. Подставляя полученное значение в параметрическое уравнение прямой, найдем координаты пересечения прямой и плоскости  .
.
8. Найти уравнение плоскости, проходящей через точку  перпендикулярно прямой
перпендикулярно прямой  .
.
Из условия направляющий вектор прямой  будет вектором нормали для искомой плоскости, т.е.
будет вектором нормали для искомой плоскости, т.е.  . Напишем уравнение плоскости, проходящею через заданную точку, с заданным вектором нормали
. Напишем уравнение плоскости, проходящею через заданную точку, с заданным вектором нормали
 . Отсюда получим общее уравнение плоскости
. Отсюда получим общее уравнение плоскости  .
.
9. Найти уравнение прямой, проходящей через точку  перпендикулярно плоскости
перпендикулярно плоскости  .
.
Из условия вектор нормали плоскости  будет направляющим вектором для искомой прямой, т.е.
будет направляющим вектором для искомой прямой, т.е.  . Напишем уравнение прямой, проходящей через заданную точку, с заданным направляющим вектором, т.е. каноническое уравнение прямой
. Напишем уравнение прямой, проходящей через заданную точку, с заданным направляющим вектором, т.е. каноническое уравнение прямой  .
.
10. Найти точку, симметричную точке  относительно плоскости
относительно плоскости  .
.
Эта задача решается в три этапа:
Напишем уравнение прямой, проходящей через точку  перпендикулярно плоскости
перпендикулярно плоскости 
 , это будет
, это будет  .
.
Находим точку пересечения прямой и плоскости  . Это будет точка
. Это будет точка  .
.
Теперь решаем задачу о нахождении координат точки симметричной данной плоскости - прямой. Координаты этой точки, которую обозначим  , вычисляются по формулам
, вычисляются по формулам  . Отсюда получим искомую точку
. Отсюда получим искомую точку  .
.
11. Найти расстояние от точки  до прямой
до прямой  .
.
Эта задача решается в три этапа:
Напишем уравнение плоскости, проходящей через точку перпендикулярно прямой 
 .
.
Вычислим проекцию точки на плоскость, для чего найдем пересечение прямой и плоскости  . Это будет точка
. Это будет точка  .
.
И наконец находим расстояние от точки до прямой  .
.

 .
.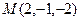 , параллельно плоскости
, параллельно плоскости  .
. . Используя условие параллельности двух плоскостей, напишем уравнение искомой плоскости:
. Используя условие параллельности двух плоскостей, напишем уравнение искомой плоскости: , отсюда
, отсюда  .
.
 , получим определитель
, получим определитель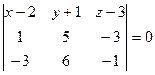 , затем – общее уравнение плоскости
, затем – общее уравнение плоскости 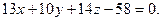
 и прямую
и прямую  .
.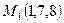 с направляющим вектором
с направляющим вектором 
 . Составим вектор
. Составим вектор  . Вектор нормали
. Вектор нормали 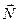 искомой плоскости должен быть перпендикулярен векторам
искомой плоскости должен быть перпендикулярен векторам 
 . Тогда, используя уравнение плоскости, проходящей через заданную точку с заданным вектором нормали, получим
. Тогда, используя уравнение плоскости, проходящей через заданную точку с заданным вектором нормали, получим  , отсюда получаем общее уравнение плоскости
, отсюда получаем общее уравнение плоскости  .
.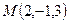 перпендикулярно плоскостям
перпендикулярно плоскостям  .
. . Вектор нормали искомой плоскости должен быть перпендикулярен этим двум векторам, т.е.
. Вектор нормали искомой плоскости должен быть перпендикулярен этим двум векторам, т.е.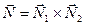

 . Тогда используя уравнение плоскости, проходящей через заданную точку с заданным вектором нормали получим
. Тогда используя уравнение плоскости, проходящей через заданную точку с заданным вектором нормали получим  ,
,  отсюда получаем общее уравнение плоскости
отсюда получаем общее уравнение плоскости 

 . Тогда используя формулу
. Тогда используя формулу  , получим
, получим  , т.е. плоскости перпендикулярны.
, т.е. плоскости перпендикулярны. ,
,  пересекаются.
пересекаются. 0. Следовательно, эти прямые пересекаются.
0. Следовательно, эти прямые пересекаются.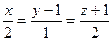 с плоскостью
с плоскостью 
 .
. в уравнение плоскости, получим
в уравнение плоскости, получим , тогда
, тогда 
 . Подставляя полученное значение в параметрическое уравнение прямой, найдем координаты пересечения прямой и плоскости
. Подставляя полученное значение в параметрическое уравнение прямой, найдем координаты пересечения прямой и плоскости  .
. перпендикулярно прямой
перпендикулярно прямой  .
. будет вектором нормали для искомой плоскости, т.е.
будет вектором нормали для искомой плоскости, т.е.  . Напишем уравнение плоскости, проходящею через заданную точку, с заданным вектором нормали
. Напишем уравнение плоскости, проходящею через заданную точку, с заданным вектором нормали . Отсюда получим общее уравнение плоскости
. Отсюда получим общее уравнение плоскости  .
. .
. будет направляющим вектором для искомой прямой, т.е.
будет направляющим вектором для искомой прямой, т.е.  . Напишем уравнение прямой, проходящей через заданную точку, с заданным направляющим вектором, т.е. каноническое уравнение прямой
. Напишем уравнение прямой, проходящей через заданную точку, с заданным направляющим вектором, т.е. каноническое уравнение прямой  .
. относительно плоскости
относительно плоскости  .
. , это будет
, это будет  .
. . Это будет точка
. Это будет точка  .
. , вычисляются по формулам
, вычисляются по формулам  . Отсюда получим искомую точку
. Отсюда получим искомую точку  .
. до прямой
до прямой  .
.
 .
. .
. .
.


