Вектори 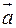 та
та 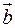 утворюють кут
утворюють кут  . Знаючи,що
. Знаючи,що 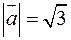 ,
, 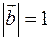 , обчислити кут між векторами
, обчислити кут між векторами  та
та  .
.
Знайти довжини діагоналей паралелограма  , якщо відомо, що
, якщо відомо, що 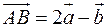 ,
,  , де
, де  ,
,  , а кут між векторами
, а кут між векторами 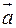 та
та 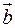 дорівнює
дорівнює  .
.
Обчислити довжину діагоналей паралелограма, побудованого на векторах  і
і  , якщо відомо, що
, якщо відомо, що  ,
, 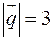 , а кут між векторами
, а кут між векторами  і
і  дорівнює
дорівнює  .
.
Відомо, що  ,
,  . Знайти, при якому значенні параметра
. Знайти, при якому значенні параметра 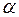 вектори
вектори  і
і 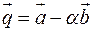 будуть взаємно перпендикулярні.
будуть взаємно перпендикулярні.
Який кут утворюють одиничні вектори 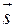 і
і  , якщо відомо, що вектори
, якщо відомо, що вектори  і
і  взаємно перпендикулярні.
взаємно перпендикулярні.
Знаючи вектори  та
та  , які лежать на сторонах
, які лежать на сторонах  , де
, де 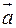 та
та 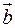 – взаємно перпендикулярні одиничні вектори, знайти кути цього трикутника.
– взаємно перпендикулярні одиничні вектори, знайти кути цього трикутника.
Знайти проекцію вектора  на вісь, яка має напрям вектора
на вісь, яка має напрям вектора 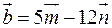 , де
, де  і
і 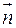 – взаємно перпендикулярні орти. Визначити кут між віссю проекцій і одиничними векторами
– взаємно перпендикулярні орти. Визначити кут між віссю проекцій і одиничними векторами  і
і 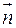 .
.
Довести, що сума квадратів медіан довільного трикутника дорівнює  суми квадратів довжин його сторін.
суми квадратів довжин його сторін.
Дано три вектори  ,
,  і
і 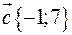 . Визначити розклад вектора
. Визначити розклад вектора  по базису
по базису 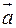 ,
, 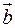 .
.
Знайти проекцію вектора  на вісь, визначену вектором
на вісь, визначену вектором  .
.
Дано розклад векторів, які служать сторонами трикутника, по двом взаємно перпендикулярним ортам:  ,
,  . Знайти довжину медіани
. Знайти довжину медіани 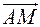 .
.
Дві сили  і
і  , які діють під кутом
, які діють під кутом 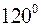 одна до одної, прикладені до однієї точки. Знайти їх рівнодіючу, якщо
одна до одної, прикладені до однієї точки. Знайти їх рівнодіючу, якщо  ,
,  .
.
Дано чотири точки  ,
, 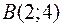 ,
,  ,
, 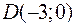 . Довести, що прямі
. Довести, що прямі  і
і  взаємно перпендикулярні.
взаємно перпендикулярні.
В прямокутній декартовій системі координат задано два вектори  ,
,  . Знайти вектор
. Знайти вектор  , який одноразово задовольняє двом умовам:
, який одноразово задовольняє двом умовам:  ,
,  .
.
Дано чотири вектори 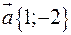 ,
, 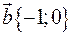 ,
,  ,
, 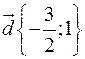 . Чи можна з них скласти трапецію?
. Чи можна з них скласти трапецію?
В прямокутній декартовій системі координат задано три вектори:  ,
,  і
і  . Знайти координати вектора
. Знайти координати вектора  .
.
Довести, що сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін.
Довести, що вектори, які співпадають з медіанами довільного трикутника, в свою чергу можуть служити сторонами другого трикутника.
Довести, що сума квадратів діагоналей будь-якого чотирикутника дорівнює сумі квадратів всіх його сторін без зчетвереного квадрата відрізка, який з’єднує середини його діагоналей.
Дано прямокутник 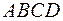 . Довести, що для довільної точки
. Довести, що для довільної точки 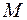 простору виконуються рівності: 1)
простору виконуються рівності: 1) 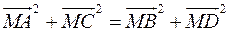 ; 2)
; 2) 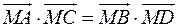 .
.
Довести, що сума квадратів довжин діагоналей трапеції дорівнює сумі квадратів довжин її непаралельних сторін, складеній з подвоєним добутком довжин основ.
Довести, що середня лінія трапеції паралельна основам і дорівнює половині їх суми.
Знайти кут між медіанами прямокутного рівнобедреного трикутника, які проведені з вершин гострих кутів.
Побудувати і обчислити  , якщо
, якщо  ,
, 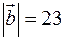 ,
,  .
.
Побудувати і обчислити 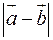 , якщо
, якщо  ,
,  ,
,  .
.
Знайти  і
і 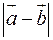 , якщо
, якщо  ,
,  ,
,  .
.
Гіпотенуза  прямокутного трикутника
прямокутного трикутника 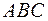 дорівнює одинці довжини. Знайти суму скалярних добутків векторів:
дорівнює одинці довжини. Знайти суму скалярних добутків векторів:  .
.
Гіпотенуза  прямокутного трикутника
прямокутного трикутника 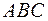 дорівнює одинці довжини. Знайти суму скалярних добутків векторів:
дорівнює одинці довжини. Знайти суму скалярних добутків векторів:  .
.
У правильному трикутнику 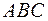 з стороною рівною одиниці довжини знайти суму скалярних добутків векторів:
з стороною рівною одиниці довжини знайти суму скалярних добутків векторів:  .
.
У правильному трикутнику 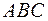 з стороною рівною одиниці довжини знайти суму скалярних добутків векторів:
з стороною рівною одиниці довжини знайти суму скалярних добутків векторів: 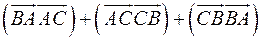 .
.
У прямокутному рівнобедреному трикутнику з катетами  і
і  проведені медіани гострих кутів. Визначити кут між ними, якщо вектори
проведені медіани гострих кутів. Визначити кут між ними, якщо вектори  і
і  одиничні.
одиничні.
Вектори  ,
, 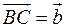 ,
,  ,
,  утворюють сторони чотирикутника
утворюють сторони чотирикутника 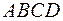 . Знайти вектор
. Знайти вектор  , який сполучає середини діагоналей
, який сполучає середини діагоналей  і
і  .
.
Знайти величину кута при вершині рівнобедреного трикутника, якщо його медіани, проведені із вершин основи, взаємно перпендикулярні.
Довести, що сума квадратів довжин діагоналей чотирикутника дорівнює подвоєній сумі квадратів довжин відрізків, які сполучають середини його протилежних сторін.
Довести, що діагоналі ромба взаємно перпендикулярні.
Довести, що діагоналі паралелограма в точці перетину діляться пополам.
Дано чотирикутник і точку 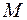 . Довести, що точки, симетричні точці
. Довести, що точки, симетричні точці 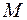 відносно середин сторін цього чотирикутника, є вершинами паралелограма.
відносно середин сторін цього чотирикутника, є вершинами паралелограма.
Довести, що середини основ трапеції і точка перетину продовжень її бічних сторін належать одній прямій.
Вектор 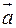 утворює з координатними осями
утворює з координатними осями  і
і 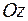 кути
кути  ,
,  . Обчислити координати вектора
. Обчислити координати вектора 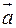 при умові, що
при умові, що  .
.
Перевірити, чи являються дані точки  ,
,  ,
,  і
і  вершинами трапеції.
вершинами трапеції.
Дано вектор  . Знайти вектор
. Знайти вектор  , колінеарний вектору
, колінеарний вектору  і протилежного з ним напрямку, якщо
і протилежного з ним напрямку, якщо 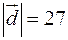 .
.
Вектори  і
і 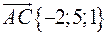 утворені відповідними сторонами трикутника
утворені відповідними сторонами трикутника 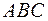 . Знайти вектори
. Знайти вектори 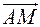 ,
,  і
і  , де
, де  ,
,  і
і  – медіани трикутника
– медіани трикутника 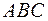 .
.
Обчислити вектор, колінеарний бісектрисі кута 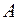 трикутника
трикутника 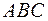 , якщо вектори
, якщо вектори 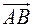 і
і  мають координати:
мають координати:  і
і  .
.
Вектор 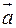 утворює з координатними осями
утворює з координатними осями 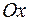 і
і  кути
кути  ,
,  . Обчислити його координати при умові, що
. Обчислити його координати при умові, що  .
.
Дано три вектора  ,
,  ,
,  . Знайти розклад вектора
. Знайти розклад вектора  по базису
по базису  ,
,  ,
,  .
.
Два вектори  ,
, 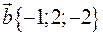 прикладені до однієї точки. Визначити координати вектора
прикладені до однієї точки. Визначити координати вектора  , напрямленого по бісектрисі кута між векторами
, напрямленого по бісектрисі кута між векторами 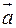 ,
, 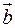 , при умові, що
, при умові, що  .
.
Визначити при яких значеннях 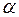 і
і  вектори
вектори  і
і  колінеарні.
колінеарні.
Дано одну з вершин трикутника  і два вектори, які співпадають з двома його сторонами:
і два вектори, які співпадають з двома його сторонами:  і
і 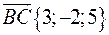 . Знайти інші вершини трикутника і вектор
. Знайти інші вершини трикутника і вектор  .
.
Вектор  , колінеарний вектору
, колінеарний вектору 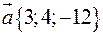 , утворює з віссю
, утворює з віссю  гострий кут. Знайти координати вектора
гострий кут. Знайти координати вектора  , якщо
, якщо  .
.
Знайти одиничний вектор, колінеарний вектору, напрямленому по бісектрисі кута  трикутника
трикутника 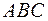 , якщо задано його вершини:
, якщо задано його вершини: 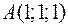 ,
,  ,
,  .
.
Вектор 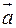 , колінеарний вектору
, колінеарний вектору 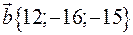 , утворює з віссю
, утворює з віссю 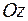 гострий кут. Знаючи, що
гострий кут. Знаючи, що  , знайти його координати.
, знайти його координати.
Вектор утворює з осями 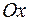 і
і 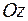 кути
кути  і
і  . Який кут він утворює з віссю
. Який кут він утворює з віссю  .
.
Визначити координати точки 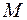 , якщо її радіус-вектор утворює з координатними осями однакові кути і його модуль дорівнює
, якщо її радіус-вектор утворює з координатними осями однакові кути і його модуль дорівнює  .
.
У площині  знайти вектор
знайти вектор  , перпендикулярний до вектора
, перпендикулярний до вектора  , що має однакову з ним довжину.
, що має однакову з ним довжину.
Дано три вектори  ,
,  і
і  . Знайти вектор
. Знайти вектор  , який одночасно задовольняє трьом рівнянням:
, який одночасно задовольняє трьом рівнянням:  ,
, 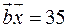 ,
,  .
.
Дано два вектори  і
і  . Знайти вектор
. Знайти вектор  , якщо він перпендикулярний до осі
, якщо він перпендикулярний до осі 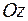 і задовольняє умовам:
і задовольняє умовам:  ,
,  .
.
Три сили  ,
,  і
і  прикладені до однієї точки. Яку роботу виконує їх рівнодіюча, якщо точка їх прикладення, рухаючись прямолінійно, переміщується із
прикладені до однієї точки. Яку роботу виконує їх рівнодіюча, якщо точка їх прикладення, рухаючись прямолінійно, переміщується із  в
в  .
.
Дано три вектори: 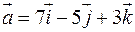 ,
,  і
і  . Знайти проекцію вектора
. Знайти проекцію вектора  на вектор
на вектор  .
.
Знайти вектор  , колінеарний вектору
, колінеарний вектору 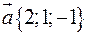 , який задовольняє умові:
, який задовольняє умові: 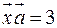 .
.
Дано вершини чотирикутника  ,
,  ,
,  і
і  . Довести, що його діагоналі взаємно перпендикулярні.
. Довести, що його діагоналі взаємно перпендикулярні.
В просторі дано три не компланарні вектори  ,
,  і
і 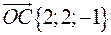 . Знайти координати вектора
. Знайти координати вектора 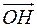 , де
, де 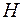 – основа перпендикуляра, опущеного з точки
– основа перпендикуляра, опущеного з точки  на площину
на площину 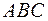 .
.
Дано трикутник  і відомі координати векторів
і відомі координати векторів  і
і 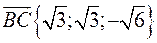 . Обчислити кути трикутника.
. Обчислити кути трикутника.
В трикутнику  , розташованому у просторі, відомі координати векторів
, розташованому у просторі, відомі координати векторів  і
і  . Визначити координати і довжину вектора
. Визначити координати і довжину вектора  , де
, де 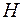 – основа перпендикуляра, опущеного з вершини
– основа перпендикуляра, опущеного з вершини 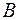 на протилежну сторону.
на протилежну сторону.
Дано трикутник з вершинами 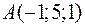 ,
,  ,
, 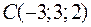 . Обчислити його зовнішній кут при вершині
. Обчислити його зовнішній кут при вершині 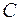 .
.
Вектор  , колінеарний вектору
, колінеарний вектору  утворює гострий кут з віссю
утворює гострий кут з віссю 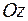 . Знаючи, що
. Знаючи, що  , знайти його координати.
, знайти його координати.
Вектор  , перпендикулярний до векторів
, перпендикулярний до векторів  і
і  , утворює з віссю
, утворює з віссю  тупий кут. Знайти координати цього вектора, якщо
тупий кут. Знайти координати цього вектора, якщо  .
.
Знайти вектор  , знаючи, що він перпендикулярний до векторів
, знаючи, що він перпендикулярний до векторів  і
і  , і задовольняє умові
, і задовольняє умові  .
.
Обчислити довжину  діагоналі паралелепіпеда, знаючи довжини
діагоналі паралелепіпеда, знаючи довжини 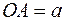 ,
,  ,
,  трьох його ребер і кути
трьох його ребер і кути  і
і  між ними.
між ними.
Якій умові повинні задовольняти вектори 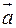 і
і 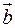 , щоб вектори
, щоб вектори  і
і  були колінеарні.
були колінеарні.
Дано модулі векторів 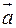 і
і 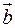 ,
, 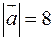 ,
, 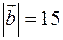 , і їх скалярний добуток
, і їх скалярний добуток  . Обчислити модуль їх векторного добутку.
. Обчислити модуль їх векторного добутку.
Обчислити площу паралелограма, побудованого на векторах  і
і 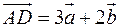 , якщо
, якщо  ,
,  і
і  .
.
Знаючи сторони трикутника 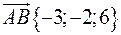 і
і  . Обчислити довжину висоти
. Обчислити довжину висоти 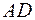 .
.
Обчислити об’єм паралелепіпеда, побудованого на векторах  ,
, 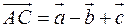 і
і  .
.
Довести, що чотири точки  ,
,  ,
,  і
і  лежать в одній площині.
лежать в одній площині.
Обчислити відстань від точки  до прямої, яка проходить через точки
до прямої, яка проходить через точки  і
і 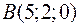 .
.
Обчислити синус кута між діагоналями паралелограма, який побудовано на даних векторах  і
і  , де
, де  ,
, 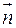 ,
,  – взаємно перпендикулярні орти.
– взаємно перпендикулярні орти.
Обчислити проекцію вектора  на вісь, напрям якої визначається вектором
на вісь, напрям якої визначається вектором  , якщо
, якщо  ,
,  ,
,  – взаємно перпендикулярні орти.
– взаємно перпендикулярні орти.
Обчислити величину кута, утвореного векторами 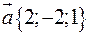 і
і  .
.
Вектор  , перпендикулярний до векторів
, перпендикулярний до векторів  і
і  , утворює з віссю
, утворює з віссю  тупий кут. Знаючи, що
тупий кут. Знаючи, що  , знайти його координати.
, знайти його координати.
Об’єм тетраедра дорівнює  куб. одиниць, три його вершини знаходяться в точках
куб. одиниць, три його вершини знаходяться в точках 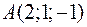 ,
,  і
і  . Знайти координати четвертої вершини
. Знайти координати четвертої вершини 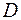 , якщо відомо, що вона належить осі
, якщо відомо, що вона належить осі  .
.
Вектор  перпендикулярний до осі
перпендикулярний до осі 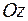 і до вектора
і до вектора  , утворює гострий кут з віссю
, утворює гострий кут з віссю 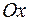 . Знаючи, що
. Знаючи, що  , знайти його координати.
, знайти його координати.
Знайти вектор  , якщо він перпендикулярний до векторів
, якщо він перпендикулярний до векторів 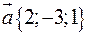 і
і  , і задовольняє умові
, і задовольняє умові  .
.
Об’єм трикутної піраміди 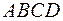 дорівнює
дорівнює  куб. Одиниці, а три її вершини знаходяться у точках
куб. Одиниці, а три її вершини знаходяться у точках 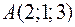 ,
,  і
і 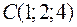 . Знайти координати четвертої вершини
. Знайти координати четвертої вершини 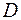 , якщо відомо, що вона належить осі
, якщо відомо, що вона належить осі 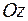 .
.
Задані чотири вектори 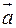 ,
, 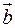 ,
,  ,
,  . Довести, що вектори
. Довести, що вектори 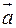 ,
, 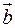 ,
,  утворюють базис, та знайти координати вектора
утворюють базис, та знайти координати вектора  , в цьому базисі та,
, в цьому базисі та, 
 ,
,  ,
,  ,
,  .
.
 ,
,  ,
,  ,
, 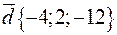 .
.
 ,
, 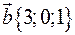 ,
,  ,
,  .
.
 ,
, 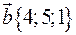 ,
,  ,
, 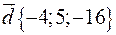 .
.
 ,
,  ,
,  ,
, 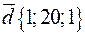 .
.
 ,
,  ,
, 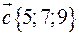 ,
,  .
.
 ,
,  ,
, 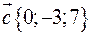 ,
,  .
.
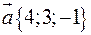 ,
,  ,
, 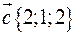 ,
,  .
.
 ,
, 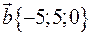 ,
, 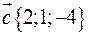 ,
, 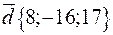 .
.
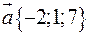 ,
,  ,
,  ,
,  .
.

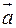 та
та 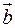 утворюють кут
утворюють кут  . Знаючи,що
. Знаючи,що 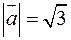 ,
, 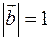 , обчислити кут між векторами
, обчислити кут між векторами  та
та  .
.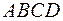 , якщо відомо, що
, якщо відомо, що 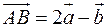 ,
,  , де
, де  ,
,  , а кут між векторами
, а кут між векторами  .
. і
і  , якщо відомо, що
, якщо відомо, що  ,
, 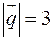 , а кут між векторами
, а кут між векторами  і
і  дорівнює
дорівнює  .
. . Знайти, при якому значенні параметра
. Знайти, при якому значенні параметра 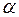 вектори
вектори  і
і 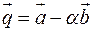 будуть взаємно перпендикулярні.
будуть взаємно перпендикулярні.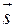 і
і  , якщо відомо, що вектори
, якщо відомо, що вектори  і
і  взаємно перпендикулярні.
взаємно перпендикулярні. та
та  , які лежать на сторонах
, які лежать на сторонах  , де
, де  на вісь, яка має напрям вектора
на вісь, яка має напрям вектора 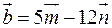 , де
, де  і
і 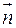 – взаємно перпендикулярні орти. Визначити кут між віссю проекцій і одиничними векторами
– взаємно перпендикулярні орти. Визначити кут між віссю проекцій і одиничними векторами  суми квадратів довжин його сторін.
суми квадратів довжин його сторін. ,
,  і
і 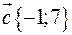 . Визначити розклад вектора
. Визначити розклад вектора  по базису
по базису  на вісь, визначену вектором
на вісь, визначену вектором  .
. ,
,  . Знайти довжину медіани
. Знайти довжину медіани 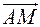 .
. і
і  , які діють під кутом
, які діють під кутом 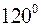 одна до одної, прикладені до однієї точки. Знайти їх рівнодіючу, якщо
одна до одної, прикладені до однієї точки. Знайти їх рівнодіючу, якщо  ,
,  .
. ,
, 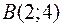 ,
,  ,
, 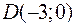 . Довести, що прямі
. Довести, що прямі  і
і  взаємно перпендикулярні.
взаємно перпендикулярні. ,
,  . Знайти вектор
. Знайти вектор  , який одноразово задовольняє двом умовам:
, який одноразово задовольняє двом умовам:  ,
,  .
.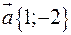 ,
, 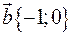 ,
,  ,
, 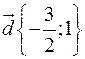 . Чи можна з них скласти трапецію?
. Чи можна з них скласти трапецію? ,
,  і
і  . Знайти координати вектора
. Знайти координати вектора  .
.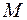 простору виконуються рівності: 1)
простору виконуються рівності: 1) 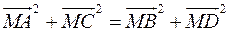 ; 2)
; 2) 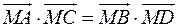 .
. , якщо
, якщо  ,
, 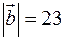 ,
,  .
.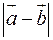 , якщо
, якщо  ,
,  ,
,  .
. ,
,  .
. прямокутного трикутника
прямокутного трикутника 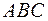 дорівнює одинці довжини. Знайти суму скалярних добутків векторів:
дорівнює одинці довжини. Знайти суму скалярних добутків векторів:  .
. .
. .
.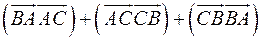 .
. і
і  і
і  одиничні.
одиничні. ,
, 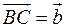 ,
,  ,
,  утворюють сторони чотирикутника
утворюють сторони чотирикутника  , який сполучає середини діагоналей
, який сполучає середини діагоналей  .
. і
і 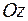 кути
кути  ,
,  . Обчислити координати вектора
. Обчислити координати вектора  .
. ,
,  ,
,  і
і  вершинами трапеції.
вершинами трапеції. . Знайти вектор
. Знайти вектор  , колінеарний вектору
, колінеарний вектору  і протилежного з ним напрямку, якщо
і протилежного з ним напрямку, якщо 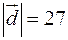 .
. і
і 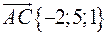 утворені відповідними сторонами трикутника
утворені відповідними сторонами трикутника  і
і  , де
, де  ,
,  і
і  – медіани трикутника
– медіани трикутника 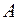 трикутника
трикутника 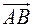 і
і  і
і  .
.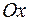 і
і  ,
,  .
. ,
,  ,
,  . Знайти розклад вектора
. Знайти розклад вектора  по базису
по базису  .
. ,
, 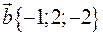 прикладені до однієї точки. Визначити координати вектора
прикладені до однієї точки. Визначити координати вектора  .
. вектори
вектори  і
і  колінеарні.
колінеарні. і два вектори, які співпадають з двома його сторонами:
і два вектори, які співпадають з двома його сторонами:  і
і 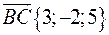 . Знайти інші вершини трикутника і вектор
. Знайти інші вершини трикутника і вектор  .
.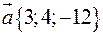 , утворює з віссю
, утворює з віссю  .
. трикутника
трикутника 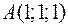 ,
,  ,
,  .
.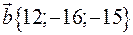 , утворює з віссю
, утворює з віссю  , знайти його координати.
, знайти його координати. і
і  .
. знайти вектор
знайти вектор  , що має однакову з ним довжину.
, що має однакову з ним довжину. ,
,  і
і  . Знайти вектор
. Знайти вектор  ,
, 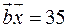 ,
,  .
. і
і  . Знайти вектор
. Знайти вектор  ,
,  .
. ,
,  і
і  прикладені до однієї точки. Яку роботу виконує їх рівнодіюча, якщо точка їх прикладення, рухаючись прямолінійно, переміщується із
прикладені до однієї точки. Яку роботу виконує їх рівнодіюча, якщо точка їх прикладення, рухаючись прямолінійно, переміщується із  в
в  .
.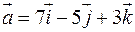 ,
,  і
і  . Знайти проекцію вектора
. Знайти проекцію вектора  на вектор
на вектор 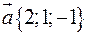 , який задовольняє умові:
, який задовольняє умові: 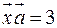 .
. ,
,  ,
,  і
і  . Довести, що його діагоналі взаємно перпендикулярні.
. Довести, що його діагоналі взаємно перпендикулярні. ,
,  і
і 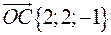 . Знайти координати вектора
. Знайти координати вектора 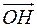 , де
, де 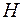 – основа перпендикуляра, опущеного з точки
– основа перпендикуляра, опущеного з точки  на площину
на площину  і
і 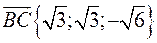 . Обчислити кути трикутника.
. Обчислити кути трикутника. і
і  . Визначити координати і довжину вектора
. Визначити координати і довжину вектора  , де
, де 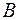 на протилежну сторону.
на протилежну сторону.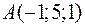 ,
,  ,
, 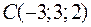 . Обчислити його зовнішній кут при вершині
. Обчислити його зовнішній кут при вершині 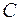 .
. утворює гострий кут з віссю
утворює гострий кут з віссю  , знайти його координати.
, знайти його координати. і
і  , утворює з віссю
, утворює з віссю  .
. і
і  , і задовольняє умові
, і задовольняє умові  .
. діагоналі паралелепіпеда, знаючи довжини
діагоналі паралелепіпеда, знаючи довжини 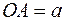 ,
,  ,
,  трьох його ребер і кути
трьох його ребер і кути  і
і  між ними.
між ними. і
і  були колінеарні.
були колінеарні.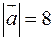 ,
, 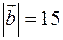 , і їх скалярний добуток
, і їх скалярний добуток  . Обчислити модуль їх векторного добутку.
. Обчислити модуль їх векторного добутку. і
і 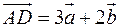 , якщо
, якщо  .
.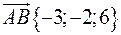 і
і  . Обчислити довжину висоти
. Обчислити довжину висоти 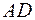 .
. ,
, 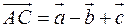 і
і  .
. ,
,  ,
,  і
і  лежать в одній площині.
лежать в одній площині. до прямої, яка проходить через точки
до прямої, яка проходить через точки  і
і 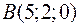 .
. і
і  , де
, де  на вісь, напрям якої визначається вектором
на вісь, напрям якої визначається вектором  , якщо
, якщо 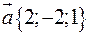 і
і  .
. і
і  , утворює з віссю
, утворює з віссю  , знайти його координати.
, знайти його координати. куб. одиниць, три його вершини знаходяться в точках
куб. одиниць, три його вершини знаходяться в точках 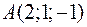 ,
,  . Знайти координати четвертої вершини
. Знайти координати четвертої вершини  , якщо відомо, що вона належить осі
, якщо відомо, що вона належить осі  , утворює гострий кут з віссю
, утворює гострий кут з віссю  , знайти його координати.
, знайти його координати.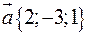 і
і  .
. куб. Одиниці, а три її вершини знаходяться у точках
куб. Одиниці, а три її вершини знаходяться у точках 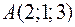 ,
,  і
і 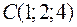 . Знайти координати четвертої вершини
. Знайти координати четвертої вершини 
 ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
, 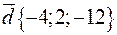 .
. ,
, 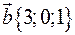 ,
,  ,
,  .
. ,
, 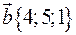 ,
,  ,
, 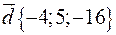 .
. ,
,  ,
,  ,
, 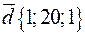 .
. ,
,  ,
, 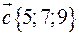 ,
,  .
. ,
,  ,
, 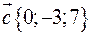 ,
,  .
.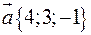 ,
,  ,
, 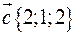 ,
,  .
. ,
, 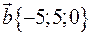 ,
, 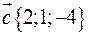 ,
, 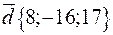 .
. ,
,  ,
,  ,
,  .
.


