На втором шаге необходимо указать, где у нас находится независимая величина Х и зависящая от нее Y . Для этого щелкаем по ярлычку вкладки «Ряд» и затем по кнопке «Добавить».

 

Рисунок 1 – “Мастер диаграмм”

Открываются поля для указания Х и Y. Ввод значений адресов в эти поля не отличаются от работы с Мастером функций (только при вводе Y предварительно сотрите условное значение “={1}”. Если Вы правильно выполните эту часть работы, на поле вверху уже появится примерный вид графика.

Следующие два шага имеют отношение к оформлению и размещению графика. На первый раз можно, ничего не меняя, просто нажимать кнопки «Далее» и «Готово». Полученный черновой вариант графика всегда можно редактировать, изменять или удалять его отдельные элементы. Обычно для этого щелкают по нужному элементу графика правой кнопкой мышки. При этом открывается контекстное меню, в котором выбирают подходящую команду.

Если правой кнопкой мышки щелкнуть по одной из точек графика, то в контекстном меню можно увидеть команду «Добавить линию тренда». Это и есть необходимая нам линия. Добавляется она тоже в два шага. На первом выбирается тип (линейный), на втором – параметры. На вкладке Параметры нам важно поставить галочки против слов: «показывать уравнение» и «поместить величину достоверности». Если из теоретических предпосылок понятно, что прямая должна проходить через начало координат (при нулевой концентрации скорость реакции, очевидно, равна нулю) поставим галочку и в данном пункте. Примерный вид графика после добавления линии тренда представлен на рисунке 5. Выведенное уравнение прямой и величины достоверности совпадает с рассчитанными ранее.

ПРИМЕР 3. В результате эксперимента была определена некоторая табличная зависимость. Выбрать и построить аппроксимирующую зависимость. Построить графики табличной и подобранной аналитической зависимости. Вычислить ожидаемое значение в указанных точках.

x1 = 0,1539, x2 = 0,2569, x3 = 0,28
X	0,15	0,16	0,17	0,18	0,19	0,20
Y	4,4817	4,4930	5,4739	6,0496	6,6859	7,3891

Решение задачи можно разбить на следующие этапы:

Ввод исходных данных и построение точечного графика (см. рис. 2).

Добавление к этому графику линии тренда.

Рассмотрим этот процесс подробно.

Рисунок 2 – “Экспериментальные значения”

Выделим экспериментальные точки на графике, щелкнем правой кнопкой мыши и воспользуемся командой Добавить линию тренда. Появившееся диалоговое окно (см. рис. 3) позволяет построить аппроксимирующую зависимость. На первой вкладке этого окна указывается вид аппроксимирующей зависимости (в нашем случае необходимо выбрать полиномиальную зависимость второй степени). На второй определяются параметры построения:

Название аппроксимирующей зависимости.

Прогноз вперед (назад) на n единиц (этот параметр определяет, на какое количество единиц вперед (назад) необходимо продлить линию тренда).

Показывать ли точку пересечения кривой с прямой Y = const.

Показывать аппроксимирующую функцию на диаграмме или нет (параметр показывать уравнение на диаграмме).

Помещать ли на диаграмму величину среднеквадратичного отклонения или нет (параметр поместить на диаграмму величину достоверности аппроксимации).

На рис. 4 изображена полученная диаграмма.

Рисунок 3 – “Линии тренда”

 

Рисунок 3 – “Линии тренда”

Для расчета ожидаемых значений в точках 0.1539, 0.2569, 0.28 введем эти значения в ячейки B4:D4. В ячейку B5 введем формулу подобранной аппроксимирующей зависимости (=371.62*B4^2-68.093*B4+6.1891) и скопируем ее в ячейки C5, D5. Фрагмент рабочего листа примет вид:

Добавим полученные расчетные значения на диаграмму. Для этого на диаграмме выделим экспериментальные значения, щелкнем правой кнопкой мыши и выберем команду Исходные данные. Добавим туда Рассчитанные значения (см. рис. 5).

Рисунок 5 – “Исходные данные”

В результате диаграмма примет вид изображенный на рис. 6. Аналогично с помощью линии тренда можно подобрать и параметры других типов зависимостей (линейной, логарифмической и экспоненциальной и т. д.).

Рисунок 6 – “Линии экспериментальных значений”

ПРИМЕР 4. В результате эксперимента получена зависимость z(t):

T	0,66	0,9	1,17	1,47	1,7	1,74	2,08	2,63	3,12
Z	38,9	68,8	64,4	66,5	64,95	59,36	82,6	90,63	113,5

Подобрать коэффициенты зависимости Z(t)=At⁴+Bt³+Ct²+Dt+K методом наименьших квадратов.

Эта задача эквивалентна задаче нахождения минимума функции пяти переменных:

(4.13)

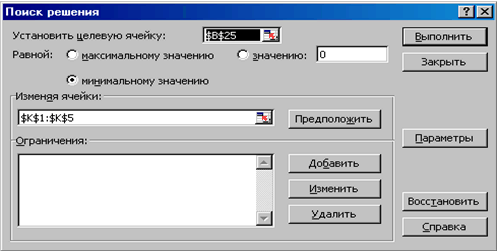
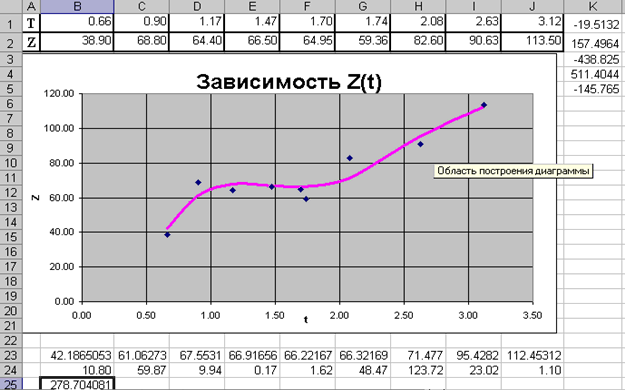
Введем табличную зависимость в рабочий лист MS Excel и построим график функции (см. рис.7)

Рассмотрим процесс решения задачи оптимизации (8). Пусть значения А, В, С, D и К хранятся в ячейках K1:K5. В ячейку B23 введем значение функции At⁴+Bt³+Ct²+Dt+K в первой точке (ячейка B1).

Получим ожидаемое значение (в начале 0) в точке B1. Затем растянем эту формулу на весь диапазон B23:J23. В ячейку B24 введем формулу, вычисляющую квадрат разности между экспериментальными и расчетными точками:

B24 = (B23-B2)^2,

и растянем ее на диапазон B24:J24. В ячейке В25 будем хранить суммарную квадратичную ошибку. Для этого введем формулу:

В25 = СУММ(B24:J24).

Теперь осталось с помощью решающего блока (Сервис Поиск решения) решить задачу оптимизации без ограничений, заполнив соответствующим образом появившееся диалоговое окно.

Рис. 7

Результатом работы решающего блока будет вывод в ячейки K1:K5 значений параметров функции At⁴+Bt³+Ct²+Dt+K. В ячейках B23:J23 получим ожидаемые значение функции в исходных точках. Поместим эти точки в виде отдельной линии на графике. В ячейке B25 будет храниться суммарная квадратичная ошибка. Рис. 8 отображает внешний вид рабочего листа MS Excel после проведенных вычислений.

По мнению авторов, использование решающего блока - это один из эффективных способов реализации метода наименьших квадратов с помощью MS Excel.

Рис. 8

 

ВАРИАНТЫ ЗАДАНИЙ

На первом рабочем листе документа MS Excel ввести исходные данные, соответствующие варианту задания. Проанализировать экспериментальную зависимость. Построить график экспериментальных точек.

На втором рабочем листе средствами MS Excel рассчитать коэффициенты регрессии, коэффициент корреляции, среднеквадратичные отклонения и суммарную ошибку. Построить в одной графической области экспериментальные точки и линию регрессии.

Третий рабочий лист должен содержать вычисление коэффициентов функциональной зависимости, соответствующей варианту задания. Расчет коэффициентов произвести аналитически при помощи метода наименьших квадратов, сведя задачу к задаче оптимизации. Построить в одной графической области экспериментальные точки и график подобранной функциональной зависимости. Определить суммарную ошибку.

На четвертом рабочем листе построить линию тренда, если это возможно. Убедится в том, что вычисленные в п.3 коэффициенты совпадают с коэффициентами линии тренда. Провести сравнительный анализ полученных результатов и построить в одной графической области график экспериментальных точек, линию регрессии и график полученной экспериментальной зависимости.

Озаглавить рабочие листы согласно тематике вычислений. Исходные данные, результаты вычислений и графики сопровождать соответствующими подписями и пояснениями.

Вариант №1. P(s)=As³+Bs²+Сs+D

s	0,00	1,00	1,50	2,00	2,50	3,00	3,50	4,00	4,50	5,00
P	10,00	50,10	39,58	15,40	23,68	33,60	57,78	100,90	149,50	256,00

Вариант № 2. G(s)=Ae^bs

s	0,5	1,5		2,5		3,5		4,5
G	3,99	5,65	6,41	7,71	11,215	17,611	27,83	38,19	39,3

Вариант № 3. K(s)=As^b

s	0,5		1,5		2,5		3,5
K	1,65	2,1		2,1	2,3	2,4	2,22	2,59

Вариант № 4. V(s)=As^bе^Cs

s	0,2	0,7	1,2	1,7	2,2	2,7	3,2
V	2,3198	2,9569	2,3999	6,4357	6,5781	6,9459	14,6621

Вариант № 5. W(s)=A/(Bs+C)

s
W	0,529	0,298	0,267	0,171	0,156	0,124	0,1	0,078	0,075

Вариант № 6. Q(s)=As²+Bs+C

s		1,25	1,5	1,75		2,25	2,5	2,75
Q	5,21	4,196	3,759	3,672	4,592	4,621	5,758	7,173	9,269

Вариант № 7. Y=x/(Ax-B)

x		3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9
Y	0,61	0,6	0,592	0,58	0,585	0,583	0,582	0,57	0,572	0,571

Вариант № 8. V=1/(A+Be^-U)

u		2,5		3,5		4,5		5,5
V	5,197	7,78	11,14	15,09	19,24	23,11	26,25	28,6	30,3

Вариант № 9. R=At^B+14,5

t
R	2,11	5,2	5,15	19,27	18,2	30,37			30,22	31,2

Вариант № 10. R=Ch²+Dh+K

h
R	0,035	0,09	0,147	0,1	0,24	0,28	0,31	0,34

Вариант №11. G=DL+K

l		0,5		1,5		2,5		3,5
G		2,39	2,81	3,25	3,75	4,11	4,45	4,85	5,25

Вариант № 12. Y=Ax³+Bx²+Cx+D

x		1,5		2,5		3,5		4,5
Y	14,5		26,9	83,75	89,9	219,1	326,1		637,5

Вариант № 13. Y=Ax³+Cx+D

x		1,5		2,5		3,5		4,5
Y	6,5	20,38	46,4	88,63	151,1	237,9		500,3	684,5

Вариант № 14. R=Ch²+K

h		1,5		2,5		3,5		4,5
R	7,5	14,25	23,7	25,86	50,7	68,25	88,5	111,5

Вариант № 15. Z=At⁴+Ct²+K

t		1,5		2,5		3,5		4,5
Z	2,2	10,6	35,6		191,1	359,2	618,7	997,9	1598,5

Вариант № 16. Z=At⁴+Bt³+Dt+K

t		1,5		2,5		3,5		4,5
Z	2,21	9,83	30,5	74,5	155,2	288,86	494,5	794,69	1214,6

Вариант № 17. Z=At⁴+Bt³+Ct²+K

t		1,5		2,5		3,5		4,5
Z	5,25	13,4	31,29	64,64	121,23	209,94	341,23	527,14

Вариант № 18. Z=At⁴+Dt+K

t	0,4	0,6	0,8		1,2	1,4	1,6	1,8
Z	0,5	1,35	2,37	3,8	5,8	8,65	12,57	18,05	0,86

Вариант № 19. Y=Ax³+D

x		0,2	0,4	0,6	0,8		1,2	1,4	1,6	1,8
Y	3,6	3,59	3,65	3,96	4,12	4,86	5,67	6,85	8,42	10,47

Вариант № 20. R=At^B

t		1,5		2,5		3,5		4,5
R	2,19	14,8	57,15	163,2	384,5	793,5		2585,5	4242,22

Вариант № 21. W(s)=1/(Bs-C)

s		1,5		2,5		3,5		4,5
W	0,19	0,17	0,15	0,14	0,13	0,12	0,11	0,1	0,9

Вариант № 22. V(s)=s^bе^Cs

s		1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9
V			52,5	83,5	130,2	202,5

Вариант № 23. Y(x)=x/(Ax+B)

x		1,5		2,5		3,5		4,5
Y	0,214	0,221	0,2237	0,2258	0,2262	0,2268	0,2275	0,2283	0,2288

Вариант № 24. V(s)=Asе^Cs

s
V	43,75	32,25	17,83	8,76		1,77	0,76	0,32

Вариант № 25. V(s)=As^bе^s

s		1,5		2,5		3,5		4,5
V	6,5	8,71	12,67	18,6	27,63	42,61	65,6	101,86

Вариант № 26. V=(A+Be^U)

u		0,5		1,5		2,5		3,5
V	3,597	4,597	5,5984	7,5987	11,269		26,5096	42,1599

Вариант №27. G(L)=D/L+K

L		1,13	1,25	1,38	1,5	1,63	1,75	1,88
G	3,8	3,2	2,6	2,2	1,8	1,6	1,4	1,3	1,1

Вариант № 28. V(s)=As^B

s		2,3	2,9	4,1	5,2	5,9	6,8	8,1	9,2
V	2,4	2,9	58,5	165,5	337,5		754,5

Вариант № 29. K(s)=Ae^Sb

s		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8
K	2,2	3,73	6,25	10,49	17,61	29,65	49,84	140,9	237,1

Вариант № 30. Z(t)=At⁵+Bt⁴+Ct³+Dt²+Kt+L

t	0,66	0,9	1,17	1,47	1,7	1,74	2,08	2,63	3,12
Z	38,9	68,8	64,4	66,5	64,95	59,36	82,6	90,63	113,5

Вариант № 31. R(T) = At⁵+Bt⁴+Ct³+Dt²+L

T
R	0,035	0,09	0,147	0,1	0,24	0,28	0,31	0,34

Вариант №32. G (t) = At⁵+Bt⁴+Dt²+Kt+L

t		0,5		1,5		2,5		3,5
G		2,39	2,81	3,25	3,75	4,11	4,45	4,85	5,25

Вариант № 33. Y (t)= At⁵+Ct³+Dt²+Kt+L

t		1,5		2,5		3,5		4,5
Y	14,5		26,9	83,75	89,9	219,1	326,1		637,5

Вариант № 34. Y (t) = At⁵+Bt⁴+Ct³+Kt+L

x		1,5		2,5		3,5		4,5
Y	6,5	20,38	46,4	88,63	151,1	237,9		500,3	684,5

Вариант № 35 R (t) = At⁵+Ct³+Kt

t		1,5		2,5		3,5		4,5
R	2,19	14,8	57,15	163,2	384,5	793,5		2585,5	4242,22

Вариант № 36. R(t) = At⁵+Dt²+Kt

t		1,5		2,5		3,5		4,5
R	2,19	14,8	57,15	163,2	384,5	793,5		2585,5	4242,22

Вариант № 37. W(T) = At⁵+Dt²+L

T		1,5		2,5		3,5		4,5
W	0,19	0,17	0,15	0,14	0,13	0,12	0,11	0,1	0,9

Вариант № 38. V= At⁵+L

T		1,1	1,2	1,3	1,4	1,5	1,7	1,8	1,9
V			52,5	83,5	130,2	202,5