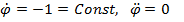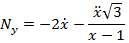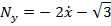Задание И5. Уравнений Лагранжа. Теорема об изменении кинетической энергии в переносном движении1. Дифференциальные уравнения движения системы найдем из уравнений Лагранжа. За обобщенные координаты выберем x и φ. Запишем соответствующие уравнения Лагранжа:
Выражение кинетической энергии системы (4.2) позаимствуем из задания И4
Производные по
Обобщенная сила
равна нулю, поскольку нет сил, имеющих составляющие вдоль Подставив (5.3) и (5.4) в (5.1) получаем дифференциальное уравнение по
Поскольку.
то
Покажем, что циклический интеграл
Подстановка данных задачи дает
что в точности совпадает с выражением (5.7). Значит (5.7) действительно выражает факт сохранение кинетического момента системы относительно оси z. Ввиду начального покоя системы
Производная от (5.7) приводит к дифференциальному уравнению по
2. Проверим уравнение относительного движения точки (1.2) в условиях задачи А. При подстановке условий задачи А:
3. Проверим закон угловой скорости тела, найденный в условиях задачи Б При подстановке условий задачи Б при отсутствии момента
что и в задании И2 при отсутствии момента. 4. Общее выражение зависимости реакции
Здесь использовано разложение выражения кинетической энергии точки Т на слагаемые по степеням относительной скорости. Справа стоит мощность внешних сил (они здесь состоят из одной реакции
Кинетическая энергия Т не содержит времени t, поэтому
Энергия
Энергия
Мощность реакции в переносном движении точки
После подстановки в теорему (5.13) получаем
Проверим выражение (для реакции Подставив эти условия в (5.19), получаем
В силу дифференциального уравнения движения точки
получаем то же выражение (1.8)
что и в задании И1.
|
:
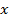
является циклической координатой, и ей соответствует циклический интеграл дифференциального уравнения по 
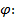
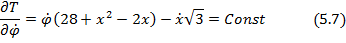
выражает факт сохранение кинетического момента системы относительно оси z. Согласно формуле (2.1) задания И2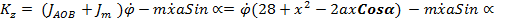
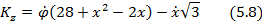
в (5.5) получаем точно такое же уравнение, как в задаче А
: 
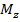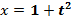в (5.7) получаем тот же закон угловой скорости
тела на точку найдем из теоремы об изменении кинетической энергии точки в переносном движении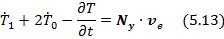
на переносном движении точки.
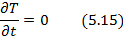
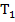, содержащая 
в первой степени и ее производная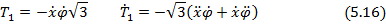
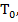содержащая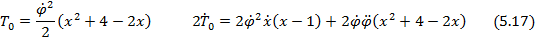 
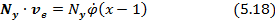
в условиях задачи А, где: 
