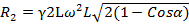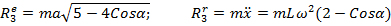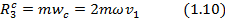Задание И1. Основное уравнения динамики относительного движения точки. Теорема о движении центра масс системы.
1.
Вращательная переносная сила инерции отсутствует, поскольку тело вращается равномерно. Центробежная сила инерции
Сила Кориолиса в проекциях на оси координат:
Отличны от нуля только проекции
Поэтому
Проектируя уравнение (1.1) на ось х, получаем дифференциальное уравнение относительного движения точки
2. Положение относительного равновесия находится в точке, где ускорение равно нулю. Это точка Р с координатой
Очевидно, что при 3. Найдем закон относительного движения и скорости точки. Это обратная задача динамики. Решение неоднородного уравнения (1.2) ищем в виде суммы общего решения однородного уравнения
Общее решение однородного уравнения
ищем в виде
Подставляя это решение в однородное уравнение, приходим к характеристическому уравнению с вещественными корнями
Решение
Частное решение ищем в виде правой части, т.е. постоянной
Полное решение уравнения (1.2)
Просьба Постоянные
Подставив (1.4) в (1.3), получим:
Иначе
Решение приобретает вид
С учетом начальных условий (1.4)
4. Найдем скорость точки в момент, когда она покидает тело. Можно было бы и закона движения определить соответствующий момент времени и подставить его в закон изменения скорости. Но лучше найти зависимость скорости точки от ее перемещения с помощью замены переменных
которая фактически приводит к теореме об изменении кинетической энергии точки. Получаем
Интегрируя, находим зависимость относительной скорости точки от ее перемещения
Из начальных условий (1.4) находим
Находим скорость при
5. Найдем закон изменения реакции тела на точку. Это прямая задача динамики. Проекция уравнения (1.1) на ось z:
дает проекцию реакции стержня на ось z
Проектируя уравнение (1.1) на ось у, находим:
Теперь проекция нормальной реакции стержня на ось у равна
В момент, когда точка покидает тело при
6. Составляющие реакции шарнира R найдем по известным ускорениям тела и точки из теоремы о движении центра масс
где
Направления составляющих изобразим на рисунке и вычислим их модуль
|

 ω
ω
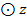

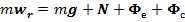 (1.1)
(1.1)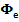 всегда направлена от оси вращения тела. Ее модуль равен
всегда направлена от оси вращения тела. Ее модуль равен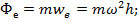
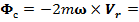
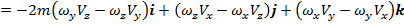

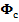 имеет проекцию только на ось у
имеет проекцию только на ось у 
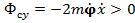
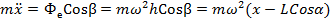
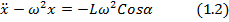
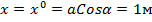
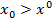 и
и 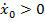 точка будет удаляться от начала О координаты
точка будет удаляться от начала О координаты 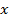 . При
. При 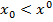 и
и 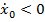 точка будет приближаться к началу О координаты х. При заданных начальных условиях точка движется в направлении оси х.
точка будет приближаться к началу О координаты х. При заданных начальных условиях точка движется в направлении оси х.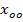 и частного решения
и частного решения 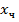 уравнения (1.2)
уравнения (1.2)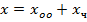
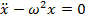
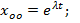
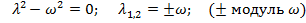
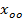 принимает вид
принимает вид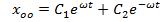
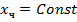 . Подставив
. Подставив 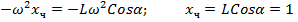
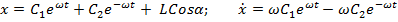 (1.3)
(1.3)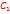 ставить при положительной степени е (!)
ставить при положительной степени е (!)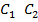 в (1.3) находим из начальных условий
в (1.3) находим из начальных условий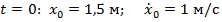 (1.4)
(1.4)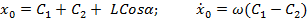
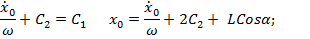
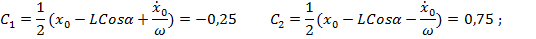

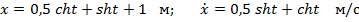 (1.5)
(1.5)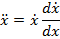
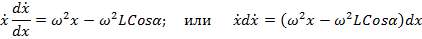
 (1.6)
(1.6)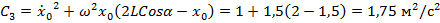
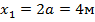
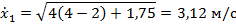
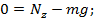
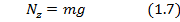
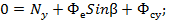
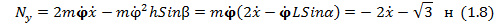
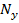 зависит от найденной относительной скорости точки (1.5).
зависит от найденной относительной скорости точки (1.5).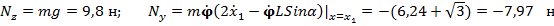 (1.9)
(1.9)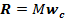

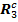
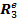
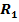
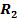
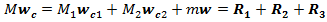
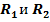 составляющие от ускорений центров тяжести стержней, а
составляющие от ускорений центров тяжести стержней, а 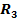 от ускорения точки. Последнее состоит из относительного, переносного и Кориолисова ускорений:
от ускорения точки. Последнее состоит из относительного, переносного и Кориолисова ускорений: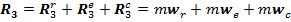
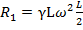 ;
;