Цели регрессионного анализа
1. Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными) 2. Предсказание значения зависимой переменной с помощью независимой(-ых) 3. Определение вклада отдельных независимых переменных в вариацию зависимой Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа. Математическое определение регрессии Строго регрессионную зависимость можно определить следующим образом. Пусть Y, X 1, X 2,..., Xp — случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений X 1 = x 1, X 2 = x 2,..., Xp = xp определено условное математическое ожидание y (x 1, x 2,..., xp) = E (Y | X 1 = x 1, X 2 = x 2,..., Xp = xp) (уравнение линейной регрессии в общем виде), то функция y (x 1, x 2,..., xp) называется регрессией величины Y по величинам X 1, X 2,..., Xp, а её график — линией регрессии Y по X 1, X 2,..., Xp, или уравнением регрессии. Зависимость Y от X 1, X 2,..., Xp проявляется в изменении средних значений Y при изменении X 1, X 2,..., Xp. Хотя при каждом фиксированном наборе значений X 1 = x 1, X 2 = x 2,..., Xp = xp величина Y остаётся случайной величиной с определённым рассеянием. Для выяснения вопроса, насколько точно регрессионный анализ оценивает изменение Y при изменении X 1, X 2,..., Xp, используется средняя величина дисперсии Y при разных наборах значений X 1, X 2,..., Xp (фактически речь идет о мере рассеяния зависимой переменной вокруг линии регрессии). Метод наименьших квадратов (расчёт коэффициентов) На практике линия регрессии чаще всего ищется в виде линейной функции Y = b 0 + b 1 X 1 + b 2 X 2 +... + bNXN (линейная регрессия), наилучшим образом приближающей искомую кривую. Делается это с помощью метода наименьших квадратов, когда минимизируется сумма квадратов отклонений реально наблюдаемых Y от их оценок
(M — объём выборки). Этот подход основан на том известном факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда Y = y (x 1, x 2,... xN). Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки:
Условие минимума функции невязки:
Полученная система является системой N + 1 линейных уравнений с N + 1 неизвестными b 0... bN Если представить свободные члены левой части уравнений матрицей
а коэффициенты при неизвестных в правой части матрицей
то получаем матричное уравнение:
Для получения наилучших оценок необходимо выполнение предпосылок МНК (условий Гаусса−Маркова). В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators) − наилучшие линейные несмещенные оценки.
21. Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду. Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.
|

 (имеются в виду оценки с помощью прямой линии, претендующей на то, чтобы представлять искомую регрессионную зависимость):
(имеются в виду оценки с помощью прямой линии, претендующей на то, чтобы представлять искомую регрессионную зависимость):

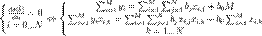


 , которое легко решается методом Гаусса. Полученная матрица будет матрицей, содержащей коэффициенты уравнения линии регрессии:
, которое легко решается методом Гаусса. Полученная матрица будет матрицей, содержащей коэффициенты уравнения линии регрессии:



