Условие завершения.
Условием завершения могут выступать:
Области применения
· Бизнес процессы · Боевые действия · Динамика населения · Дорожное движение · ИТ-инфраструктура · Логистика · Пешеходная динамика · Производство · Рынок и конкуренция
GPSS (General Purpose Simulation System) GPSS - язык программирования, используемый для имитационного моделирования (процессное моделирование) различных систем, в основном систем массового обслуживания.
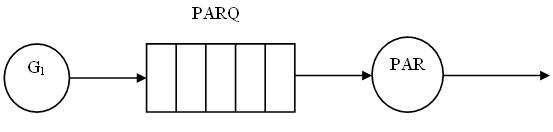
Пример задачи Интервалы прихода клиентов в парикмахерскую с одним креслом распределены равномерно: 18÷6 мин. Время стрижки также распределено равномерно: 16÷4 мин. Клиенты приходят в парикмахерскую, стригутся в порядке «первым пришел — первым обслужен» и затем уходят. Модель парикмахерской на GPSS должна обеспечить сбор статистических данных об очереди. Необходимо промоделировать работу в течение 8 часов модельного времени.
; первый сегмент программы 10 GENERATE 18,6; приход клиентов 20 QUEUE PARQ; присоединение к очереди 30 SEIZE PAR; переход в кресло парикмахера 40 DEPART PARQ; уход из очереди 50 ADVANCE 16,4; обслуживание у парикмахера 60 RELEASE PAR; освобождение парикмахера 70 TERMINATE; уход из парикмахерской ; второй сегмент прог раммы 80 GENERATE 480; транзакт приходит в момент времени, равный 480 90 TERMINATE 1; завершение моделирования
Анализ результатов Прибор 1. Парикмахер был занят обслуживанием 27 раз, ENTRIES (число входов)=27. 2. Он был занят в течение 88.5% времени, UTIL. (загрузка)=0.885. 3. Среднее время интервала обслуживания парикмахера равно 15,74 мин, AVE_TIME (среднее время)=15.74. 4. После окончания интервала времени, равного 8 ч, в кресле остался один необслуженный клиент, AVAILABLE=1. Очередь 1. В очереди к парикмахеру никогда не было более одного клиента, MAX (максимальное содержимое)=1. 2. Содержимое очереди на момент окончания моделирования равно 0, CONT. (содержимое)=0. 3. Всего в очередь входило 27 клиентов, ENTRIES (число входов)=27. 4. Среди этих 27 входов было 8 нулевых, ENTRIES(0) (число нулевых входов)=8. 5. Среднее число клиентов, находившихся в очереди, равно 0,23, AVE_CONT (среднее содержимое)=0.23. 6. Среднее время пребывания клиентов в очереди равно 4.11, AVE_TIME (среднее время) =4.11. 7. Среднее время пребывания клиентов в очереди (исключая нулевые входы) равно 5.84, AVE(-0) (среднее время, исключая нулевые входы) =5.84
Выводы. Преимущества имитационного моделирования Применение имитационных моделей дает множество преимуществ по сравнению с выполнением экспериментов над реальной системой и использованием других методов.
Стоимость. Допустим, компания уволила часть сотрудников, что в дальнейшем привело к снижению качества обслуживания и потери части клиентов. Принять обоснованное решение помогла бы имитационная модель, затраты на применение которой состоят лишь из цены программного обеспечения и стоимости консалтинговых услуг.
Время. В реальности оценить эффективность, например, новой сети распространения продукции или измененной структуры склада можно лишь через месяцы или даже годы. Имитационная модель позволяет определить оптимальность таких изменений за считанные минуты, необходимые для проведения эксперимента.
Повторяемость. Современная жизнь требует от организаций быстрой реакции на изменение ситуации на рынке. Например, прогноз объемов спроса продукции должен быть составлен в срок, и его изменения критичны. С помощью имитационной модели можно провести неограниченное количество экспериментов с разными параметрами, чтобы определить наилучший вариант.
Точность. Традиционные расчетные математические методы требуют применения высокой степени абстракции и не учитывают важные детали. Имитационное моделирование позволяет описать структуру системы и её процессы в естественном виде, не прибегая к использованию формул и строгих математических зависимостей.
Наглядность. Имитационная модель обладает возможностями визуализации процесса работы системы во времени, схематичного задания её структуры и выдачи результатов в графическом виде. Это позволяет наглядно представить полученное решение и донести заложенные в него идеи до клиента и коллег.
Универсальность. Имитационное моделирование позволяет решать задачи из любых областей: производства, логистики, финансов, здравоохранения и многих других. В каждом случае модель имитирует, воспроизводит, реальную жизнь и позволяет проводить широкий набор экспериментов без влияния на реальные объекты.
|