СТАТИСТИЧЕСКОЕ ПРИЛОЖЕНИЕ: ОПРЕДЕЛЕНИЕ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ И ПАРАМЕТРОВ НА ОСНОВЕ ВЫБОРОЧНЫХ СТАТИСТИК. СРЕДНЕЕ И СТАНДАРТНОЕ ОТКЛОНЕНИЕ
Определение среднего в популяции (генеральной совокупности) В эксперименте по определению времени реакции, описанном в приложении к главе 1, были взяты результаты действительного эксперимента. Предполагалось, что они представляют такие данные, которые могли бы быть получены в эксперименте с полной внутренней валидностью. Так, среднее время реакции на световой сигнал по 17 пробам представляло среднее, которое можно было бы получить в эксперименте с неограниченным числом проб. Мы используем среднее для ограниченной выборки проб, чтобы сделать вывод о достаточно большой (вплоть до неограниченной) популяции проб. Такая популяция называется генеральной совокупностью. Среднее по генеральной совокупности таких, например, данных, как ВР, обозначается Мх. Такую характеристику генеральной совокупности называют параметром. Среднее, действительно вычисленное нами для данной выборки, называется статистикой, и обозначается Мх. Является ли статистика Мх наилучшей оценкой параметра Мх, которую мы можем получить на основе нашей выборки проб? Ответ — без доказательства — да. Но прежде чем вы решите, что это всегда так, давайте перейдем, к стандартному отклонению, где дело обстоит иначе. Вычисление стандартного отклонения Обычно помимо среднего значения оценок мы хотим знать еще кое-что, а именно, какова несистематическая вариация оценок от пробы к пробе. Наиболее распространенный способ измерения несистематической вариации состоит в вычислении стандартного отклонения. Для этого, вы определяете, насколько каждая оценка (т. е. X) больше или меньше среднего (Мх). Затем вы возводите в квадрат каждую разность (X-Мх) и складываете их. Вслед за этим вы делите эту сумму на N число проб. Наконец, вы извлекаете квадратный корень из этого среднего. Это вычисление представлено формулой с использование символа σх для обозначения стандартного отклонения:
Эту формулу можно сократить, введя маленькое х для обозначения (X-Мх). Тогда формула выглядит так:
Давайте выпишем данные по условию А из приложения к главе I и одновременно произведем по ним вычисления, указываемые формулой для σх
Поскольку
То
Оценка стандартного отклонения генеральной совокупности Для определения среднего генеральной совокупности, которое могло бы быть получено в бесконечном эксперименте, наилучшей оценкой фактически было среднее по выборке. Иначе обстоит дело со стандартным отклонением. В любом наборе реальных проб имеет место меньшее число результатов с очень высокими или очень низкими значениями, чем в генеральной совокупности. А поскольку стандартное отклонение является мерой разброса оценок, то его величина, определенная на основе выборки, всегда меньше параметра генеральной совокупности сигма σх. Более точная, оценка стандартного отклонения для генеральной совокупности находится по формуле
Или
Для наших числовых данных:
В некоторых экспериментах высказывается гипотеза, что поведение в одном условии более вариативно, чем в другом. Тогда целесообразнее сравнивать стандартные отклонения, а не средние. Если для обоих условий N одно и то же, можно сравнивать между собой сигмы. Однако когда N различны, сигма для условия с меньшим N дает более заниженную оценку такого параметра генеральной совокупности, как стандартное отклонение. Поэтому следует сравнивать два S. Таблица, которая приводится ниже, поможет вам запомнить эти положения и формулы.
Задача: Вычислите σх и Sх для условия Б. Ответ: σБ = 15,9; σБ = 16,4. Статистическая таблица 1
|

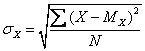 (2.1)
(2.1) (2.1A)
(2.1A)
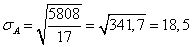 мс.
мс.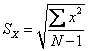 (2.2)
(2.2)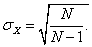 (2.2А)
(2.2А)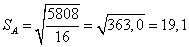 мс.
мс.







