СТАТИСТИЧЕСКОЕ ПРИЛОЖЕНИЕ: КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Стандартные оценки
Самая простая формула для вычисления коэффициента корреляции между двумя выборками оценок задается с помощью стандартных оценок. Эта формула дает также наиболее ясное представление о значении коэффициента корреляции. Вот почему в этом приложении вводится понятие стандартной оценки. Кроме того, стандартные оценки, полученные в различных тестах, можно сравнить между собой. Так, если вы скажете кому-либо, что по истории вы получили тестовую оценку 38, а по английскому языку — 221, он мало что поймет. Однако этот «кто-то», если он читал данное приложение, получит точную информацию из сообщения, что ваша стандартная оценка по истории ранка +2,1, а по английскому языку —1,3.
Вы уже знаете, что (первичная) тестовая оценка какого-либо испытуемого в группе обозначается через X. Тестовая же оценка данного конкретного испытуемого обозначается с помощью индекса. Так, например, тестовая оценка испытуемого 3 записывается как Х3. Вы также знакомы с отклонением оценки от среднего х=Х—Мх. Отклонение оценки испытуемого 3 записывается как xз=Хз—Мх. Если отклонение оценки испытуемого разделить на стандартное отклонение σх распределения оценок, то оно преобразуется в стандартную оценку (или z-оценку).
Допустим, что испытуемый 3 имеет (первичную) тестовую оценку 60. Средняя оценка для группы равна 49 и стандартное отклонение оценок равно 12, т. е. Х3=60, Мх=49, σх=12. Прежде всего xз=60—49=+11. Давайте теперь вычислим zx, т. е. найдем стандартную оценку для испытуемого 3:
zx=x/σх. (9.1)
Следовательно,
Поскольку стандартные оценки редко имеют величину больше +2 и меньше —2, то вы узнаете, что оценка именно этого испытуемого лежит примерно посередине между средней и наивысшей оценкой в группе.
Рабочие оценки, такие, например, как оценки качества работы контролеров, которые необходимо скоррелировать с тестовыми оценками, обычно обозначаются символом Υ вместо X. Тогда отклонение оценки обозначается через у, а стандартная рабочая оценка — zY. Итак, мы говорим о нахождении корреляции между X и Υ тогда, когда каждый испытуемый в группе имеет оценку X и оценку Υ. Коэффициент корреляции обозначается символом rXY.
Вычисление Rxy
Для вычисления коэффициента оды снова воспользуемся ранее приводившимися данными. Возьмем данные для условия А как тестовые оценки 17 испытуемых, а данные для условия Б как рабочие оценки для тех же испытуемых. Однако чтобы подчеркнуть относительный характер стандартных оценок, умножим каждое значение для условия Б на 10. К счастью, мы уже сделали много вычислений, необходимых для (получения rXY· Для тестовых оценок «мы просто используем полученные ранее — среднее и стандартные отклонения. Для условия Б полученные — среднее и стандартные отклонения нужно просто умножить на 10.
Вы видите, что тестовая оценка (X) первого испытуемого S1 была 223, а его рабочая оценка —1810. Сдвинувшись по этой строке от обоих концов к середине, мы обнаружим, что x равно +38 (т. е. 223—185) и у равно +190 (т. е. 1810—1620). Далее, видим, что zX равно 2,054 (т. е. +38, деленное на 18,5), a zy равно + 1,195 (т. е. 190, деленное на 159). И наконец, в среднем столбце мы находим произведение zx на zy, которое равно +2,455.
Тестовые оценки помещены в приводимой ниже таблице во втором столбце слева, а рабочие оценки — во втором столбце справа. Они обозначены как X и У соответственно
Σzxzy = +7,336; rxy= +0,432. Такие же вычисления, сделанные для остальных 16 испытуемых, заполняют всю остальную таблицу. Ниже этих данных приведены величины средних и стандартных отклонений. Еще ниже в центре дается сумма по столбцу zxzy, равная +7,336. Это число, деленное на число испытуемых — 17, и дает величину коэффициента корреляции, равную +0,432. В случае, если вам не хочется запоминать все эти термины, вы можете обратиться к следующей формуле для расчета коэффициента корреляции:
или для наших данных
Диаграмма разброса (корреляционное поле) На рис. 9.4 показана диаграмма разброса, каждая точка которой представляет одного испытуемого. Значения шкал даны в единицах стандартных оценок г.
Рис. 9.4. Корреляционное поле. Масштабы осей равны и представлены в единицах стандартных оценок При таких осях наклон линии предсказывания прямо показывает величину rXY. В нашем случае rXY равно +0,432. Это значение наклона линии: на каждое смешение на единицу вправо точки линии поднимаются вверх на 0,432 единицы. Так, если данный испытуемый имеем значение zX, равное +1, то предсказываемое значение zX для него равно +0,432. Таким образом, предсказываемая величина значительно ближе к среднему распределения, чем та величина, на основе которой делалось предсказание. Поэтому говорят, что предсказания стремятся (регрессируют) к среднему, и линия предсказания называется линией регрессии X на Y. Более точно, это предсказание zY по zX. Вы можете заметить, что линия предсказания проходит через пересечение точек zX = 0 и zY = 0. Обе эти точки представляют средние значения соответствующих распределений. Это справедливо, независимо от значения величины rXY. Если испытуемый оказывается в точке среднего по X, то наилучшим.предсказанием всегда будет среднее по Y. Далее видно, что если оценка будет выше среднего по X (положительное значение zX), то предсказываемая оценка будет также выше среднего по Y (положительное значение zY). Точно так же для X ниже среднего значения предсказываемая оценка Y будет ниже среднего значения по Y. И наконец, чем выше величина rXY. тем меньше регрессия предсказания. В случае полной корреляции линия предсказания будет иметь наклон +1. Так, если, например, zX равно +1,5, то предсказываемое zY тоже будет равно +1,5, а если zX равно —0,8, то zY тоже будет равно —0,8. При полной корреляции регрессия к среднему отсутствует. С другой стороны, если корреляция равна 0, то линия будет иметь нулевой наклон, т. е. она будет представлять собой горизонтальную линию. Она будет проходить на уровне zY=0, т. е. среднего значения по Y. Поэтому, какая бы ни была величина zX, наилучшее предсказание всегда будет zY = 0. Следовательно, при нулевой корреляции все предсказываемые значения регрессируют к среднему. Все это может быть представлено посредством следующей формулы:
Эта формула показывает, что стандартную оценку для выборки Y можно получить, умножив стандартную оценку для выборки X на коэффициент корреляции между X и Y. Например, для испытуемого, имеющего стандартную оценку zX, равную +0,50 с коэффициентом корреляции 0,70, получим
Задача: Вычислите rXY для данных в задаче, приведенной в статистическом приложении к главе 6. Используйте условие В для X и условие Г для Y. Ответ: rXY = 0,576.
|

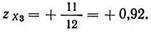
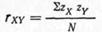 (9.2)
(9.2)

 (9.3)
(9.3)



