Вычисление производных
При написании сложных формул, особенно использующих вложенные функции, использование мастера функций - наилучшее решение. Он очень облегчает и ускоряет ввод формул, и делает многие вещи за нас: автоматически вставляет знак "равно", имя функции, круглые скобки, расставляет точки с запятой. Позволяет просматривать значение ссылок и результаты промежуточных вычислений. В одну функцию можно вставить другую функцию. Допускается до 7-ми уровней вложения функций (в Office 2007 -- до 64). Например, СУММ(СТЕПЕНЬ(2,3);5)Для этого из окна одной функции нужно выбрать в адресном окне другую функцию, ввести необходимые аргументы. После этого окно мастера функций для предыдущей функции (в этом примере "СУММ") сменится на окно для вставляемой функции ("СТЕПЕНЬ"), и ее название в формуле сделается жирным. Чтобы опять вернуться к окну для функции "СУММ", достаточно просто щелкнуть в строке формул на ее названии, и окно для степени сменится на окно для "СУММ". После этого функция "СУММ" в названии станет жирной, показывая, что в данный момент окно открыто именно для нее. Вычисление логарифмов. Преобразование логарифмических выражений
ВАРИАНТ 2
ВАринт 3
В варианте №7 не надо решать №3, №6.
ответы
Вычисление производных
1. Закон движения точки по прямой задается формулой а) б) Вычислите мгновенную скорость точки в момент
2. Закон движения точки по прямой задается формулой а) б) Вычислите мгновенную скорость точки в момент
3. Закон движения точки по прямой задается формулой а) б) Вычислите мгновенную скорость точки в момент
4. Закон движения точки по прямой задается формулой а) б)
5. Закон движения точки по прямой задается формулой а) б)
6. Найдите производную функции: 1) 2) 3) 7. Найдите производную функции: 1) 2) 3)
8. Найдите производную функции: 1) 2) 3) 4)
9. Найдите производную функции: 1) 2) 3) 4) 5) 6) 7) 8)
10. Найдите производную функции: 1) 2) 3) 4) 5) 6) 7) 8)
11. Существует ли производная заданной функции в указанных точках? Если да, то найдите значения производных: 1) 2)
12. При каких значениях параметров
а) непрерывна на всей числовой прямой; б) дифференцируема на всей числовой прямой?
13. При каких значениях параметров
а) непрерывна на всей числовой прямой; б) дифференцируема на всей числовой прямой?
14. Строится мост параболической формы, соединяющий точки А и В, расстояние между которыми 200 м. Въезд на мост и съезд с моста должны быть прямолинейными участками пути, направленными к горизонту под углом a = 15°. Указанные участки должны быть касательными к параболе. Составьте уравнение профиля моста в заданной на рисунке системе координат.
15. а) При каких значениях параметра б) При каких значениях параметра
|











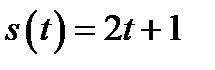 , где
, где 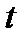 — время (в секундах),
— время (в секундах), 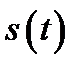 — отклонение точки в момент времени
— отклонение точки в момент времени 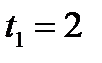 с до момента:
с до момента: с; в)
с; в)  с;
с; с; г)
с; г)  с.
с. с.
с. , где
, где  с до момента:
с до момента: с; в)
с; в)  с;
с;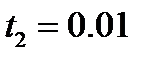 с; г)
с; г)  с.
с. с.
с. , где
, где  с; в)
с; в) 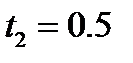 с;
с; с; г)
с; г)  с.
с. , где
, где  ; в)
; в)  ;
; ; г)
; г) 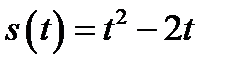 .
. , где
, где  , если:
, если: с; в)
с; в)  с;
с; с; г)
с; г)  с.
с. ; 4)
; 4)  ; 7)
; 7)  ; 10)
; 10)  ;
; ; 5)
; 5)  ; 8)
; 8)  ; 11)
; 11)  ;
;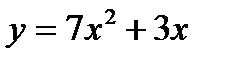 ; 6)
; 6)  ; 9)
; 9)  ; 12)
; 12)  .
. ; 4)
; 4)  ; 7)
; 7) 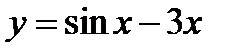 ; 10)
; 10) 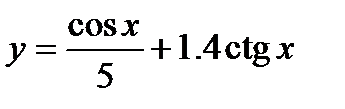 ;
; ; 5)
; 5)  ; 8);
; 8);  11)
11)  ;
; ; 6)
; 6)  ; 9)
; 9) 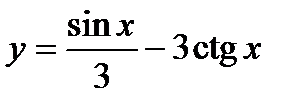 ; 12)
; 12)  .
. ; 5)
; 5)  ; 9)
; 9) 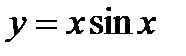 ;
; ; 6)
; 6) 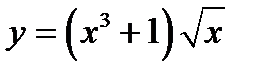 ; 10)
; 10)  ;
; 7)
7)  ; 11)
; 11) 
 ; 8)
; 8)  ; 12)
; 12)  .
. ; 9)
; 9)  ;
; ; 10)
; 10)  ;
; ; 11)
; 11)  ;
; ; 12)
; 12)  ;
; ; 13)
; 13)  ;
; ; 14)
; 14) 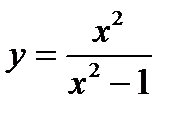 ;
; ; 15)
; 15)  ;
; ; 16)
; 16)  .
. ; 9)
; 9)  ;
; ; 10)
; 10)  ;
; ; 11)
; 11)  ;
; ; 12)
; 12)  ;
;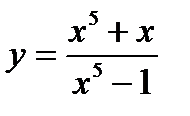 ; 13)
; 13) 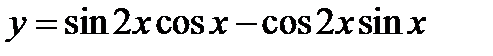 ;
; ; 14)
; 14) 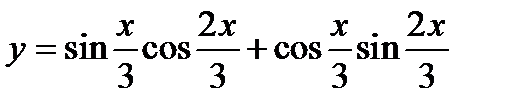 ;
;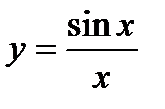 ; 15)
; 15)  ;
; ; 16)
; 16)  .
. ,
,  ; 3)
; 3) 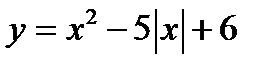 ,
, 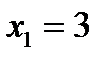 ,
,  .
. ,
,  ; 4)
; 4)  ,
,  ,
,  ,
, 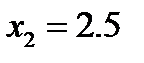 .
. и
и  функция
функция


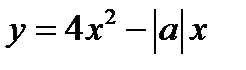 , проведенные в точках его пересечения с осью
, проведенные в точках его пересечения с осью  , образуют между собой угол 60°?
, образуют между собой угол 60°? , проведенные в точках его пересечения с осью
, проведенные в точках его пересечения с осью 


