Продукционная модель
В 1972-1973 гг. Ньюэл и Саймон (авторы идеи экспертных систем) показали, что человек в ходе рассуждений и деятельности использует правила, подобные продукциям, т.е. делает заключения по схеме "условие->следствие" и действует по схеме "ситуация->действие". Тогда же Ньюэл предложил использовать продукционные системы для моделирования процессов принятия решений в системах искусственного интеллекта. Сегодня системы продукций (наряду с сетевыми моделями) являются наиболее популярными средствами представления знаний в системах искусственного интеллекта. Продукционная модель, или модель, основанная на правилах, позволяет представить знания в виде предложений типа: Если (условие A), то (действие B), обозначаемое логическим выражением вида A→B. Под, условием понимается некоторое предложение-образец, по которому осуществляется поиск в базе знаний, а под действием - действия, выполняемые при успешном исходе поиска (они могут быть промежуточными, выступающими далее как условия, и терминальными или целевыми, завершающими работу системы). При использовании продукционных моделей для представления знаний создается продукционная система - набор продукций, организованный по определенному принципу. Для систем продукций создаются также определенные процедуры управления их функционированием, на которые обычно возлагается решение следующих задач: б) разрешение конфликтов между правилами (с учетом приоритетов, эффективности, эвристик) и выбор правила для применения (правила, которое должно действовать);
Рис. 3.1. Продукционная система Продукционная система, как указывалось выше, состоит из трех основных компонентов. Первый из них — это набор правил, используемый как база знаний, поэтому его еще называют базой правил. Следующим компонентом является рабочая память (или память для кратковременного хранения), в которой хранятся предпосылки, касающиеся конкретных задач предметной области, и результаты выводов, полученных на их основании, и наконец, следует механизм логического вывода, использующий правила в соответствии с содержимым рабочей памяти (рис. 3.1). Существуют два способа вывода заключений – путем построения прямой или обратной цепочки рассуждений. В концепции глобальной базы данных может быть реализован каждый из этих способов. При этом в прямых цепочках рассуждений вывод очередного заключения осуществляется путем сопоставления данных, содержащихся в базе данных, с левыми частями правил, и если находится правило, где сопоставление происходит, правая часть этого правила в качестве заключения по этому правилу помещается в базу данных (или исполняется предписываемое правой частью этого правила действие, соответствующим образом изменяющее содержимое базы данных). В обратных цепочках рассуждений вывод начинается от поставленной цели. Если находится правило, правая часть (заключение) которого сопоставляется с этой целью, то левая часть (посылка) правила принимается за подцель. Этот процесс обратного вывода повторяется до тех пор, пока не будет получено совпадение подцелей с данными. Для того чтобы показать, как взаимодействуют эти элементы, рассмотрим несложный пример. Допустим, что данные, записываемые в рабочую память, представляют собой образцы в виде наборов символов. Например, «намерение — отдых», «место отдыха — горы» и т. п. Правила, накапливаемые на базе правил, отражают содержимое рабочей памяти. В их условной части находятся либо одиночные образцы, либо несколько условий, соединенных предлогом «и», а в заключительной части — образцы, дополнительно регистрируемые в рабочей памяти, Рассмотрим два примера подобных правил.
Рис. 3.2. Представление правила графом
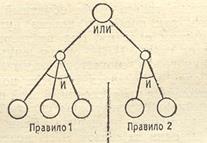
Рис.3.3. Заключение, выводимое с помощью нескольких правил
Правило 1. ЕСЛИ «намерение — отдых» и «дорога ухабистая» ТО «использовать джип» Правило 2. ЕСЛИ «место отдыха — горы» ТО «дорога ухабистая»
После того, как в рабочую память записываются образцы «намерение — отдых» и «место отдыха— горы», рассматривается возможность применения этих правил. Сначала механизм вывода сопоставляет образцы из условной части правила с образцами, хранимыми в рабочей памяти. Если все образцы имеются в рабочей памяти, условная часть считается истинной, в противном случае — ложной. В данном примере образец «намерение — отдых» существует в рабочей памяти, а образец «дорога ухабистая> отсутствует, поэтому его условная часть считается ложной. Что касается правила 2, то его условная часть истинна. Поскольку в данном случае существует только одно правило с истинной условной частью, то механизм вывода сразу же выполняет его заключительную часть и образец «дорога ухабистая» заносится в рабочую память. При попытке вторично применить эти правила получается, что можно применить лишь правило 1, поскольку правило 2 уже было применено и выбыло из числа кандидатов. К этому времени содержимое рабочей памяти было дополнено новым образцом — результатом применения правила 2, поэтому условная часть правила 1 становится истинной, и содержимое рабочей памяти пополняется образцом его заключительной части — «использовать джип». В итоге правил, которые можно было бы применять, не остается, и система останавливается. В приведенном примере для получения вывода совершалась работа по извлечению предварительно записанного содержимого рабочей памяти, применению правил и дополнения данных, помещаемых в память. Такие выводы называются прямыми. Напротив, способ, при котором на основании фактов, требующих подтверждения, чтобы выступать в роли заключения, исследуется возможность применения правила, пригодного для подтверждения, называется обратным выводом. Чтобы пояснить этот способ, вернемся к знакомому уже примеру. Допустим, что цель — это “использовать джип», и исследуем сначала возможность применения правила 1, подтверждающего этот факт. Поскольку образец «намерение — отдых» из условной части правила 1 уже занесен в рабочую Память, то для достижения цели достаточно подтвердить факт «дорога ухабистая». Однако если принять образец «дорога ухабистая» за новую цель, то потребуется правило, подтверждающее этот факт. Поэтому исследуем возможность применения правила 2. Условная часть этого правила в данный момент является истинной, поэтому правило 2 можно сразу же поменять, рабочая память при этом пополнится образцом «дорога ухабистая», и в результате возможности применения правила 1 подтверждается цель «использовать джип». В случае обратного вывода условия останова системы очевидны: либо достигается первоначальная цель, либо кончаются правила, применимые для достижения цели в ходе вывода. Что касается прямого вывода, то, как было сказано выше, отсутствие применимых правил также является условием останова системы. Однако система останавливается и при выполнении некоторого условия, которому удовлетворяет содержимое рабочей памяти, например путем проверки появления образца «использовать джип». В приведенном примере на каждом этапе прямого вывода можно было применять только одно правило, поэтому особых проблем здесь не возникало. В общем случае на каждом этапе вывода таких правил несколько, и тут возникает проблема выбора подходящего из них. Для наглядности дополним этот пример следующим правилом.
Правило 3. ЕСЛИ «намерение — отдых» ТО «нужна скорость»
Кроме того, введем еще одно условие останова системы - появление в рабочей памяти образца «использовать джип». Итак, вследствие добавления нового правила на первом этапе вывода появлялась возможность применять правило 2 и правило 3. Если сначала применить правило 2, то на следующем этапе можно будет применять правило 1 и правило 3. Если на этом этапе применить правило 1, то выполняется условие останова системы, но если прежде применить правило 3, то потребуется еще один этап вывода, поэтому выбирают правило 1 и система останавливается. Этот несложный пример показывает, что выбор применяемого правила оказывает прямое влияние на эффективность вывода. В реальной системе, требующей подготовки множества правил, это поистине грандиозная проблема. Если на каждом этапе логического вывода существует множество применимых правил, то это множество носит название конфликтного набора, а выбор одного из них называется разрешением конфликта. Эта же проблема характерна и для систем с обратным выводом, т.е. когда для достижения одной цели рассматривается применение множества правил, то также возникает проблема выбора одного из них. Например, дополним предыдущий пример следующим правилом.
Правило 4. ЕСЛИ «место отдыха — пляж» ТО «дорога ухабистая»
Если на основании этого условия подтверждается цель «использовать джип», то для достижения первоначальной цели достаточно применить только одно правило 1, однако, чтобы подтвердить новую цель «дорога ухабистая», открывающую возможность применения правила 1, нужно выбрать либо правило 2, либо правило 4. Если сначала применить правило 2, - то это будет самый удачный выбор, поскольку сразу, же можно применить и правило 1. С другой стороны, если попытаться применить правило 2, то, поскольку, образца «место отдыха — пляж», который является условием правила 4, в рабочей памяти не существует, и кроме того, не существует правила, подтверждающего его, данный выбор является неудачным. И лишь со второго захода, применяя правило 2, можно подтвердить цель «дорога ухабистая». Обратите внимание на тот факт, что при обратном выводе применение правила 3, которое не оказывает прямого влияния на достижение цели, не принималось в расчет с самого начала. Таким образом, для обратных выводов характерна тенденция исключения из рассмотрения правил, не имеющих прямого отношения к заданной цели, что позволяет повысить эффективность вывода. До сих пор рассматривалась базовая структура продукционных систем продукций, однако на практике для построения действующих систем необходимы разнообразные дополнительные средства. Прежде всего в некоторых случаях недостаточно записи в рабочую память лишь одного образца и возникает необходимость управления данными, уточняющими смысл. В таких случаях довольно часто используется способ представления конкретных данных с помощью триплета: объект-атрибут-значение. По этому способу отдельная субстанция из предметной области (человек, предмет и т. п.) рассматривается как один объект, и можно считать, что данные, хранимые в рабочей памяти, показывают значения, которые принимают атрибуты этого объекта. Например, данные “собака 1 кличка Джон» показывают тот факт, что существует (некоторая) собака и кличка этой собаки — Джон. Одним из преимуществ, связанных с внедрением структуры объект-атрибут-значение, является уточнение контекста, в котором применяется правило. Например, правило, единое для всех объектов «собака», должно быть пригодным для применения независимо от того, идет ли речь о собаке по кличке Джон или о другой собаке по кличке Мэри. Здесь следует отметить, что в примере, изложенном ранее, было разъяснено, что одно и то же правило нельзя использовать повторно. Однако когда существует несколько объектов, для которых пригодно одно и то же правило, то оно вполне может быть применено для каждого объекта, но не более одного раза. Эта проблема называется проблемой контекста применения правила, кроме того, объект применения правила еще называют контекстом применения правила. 3.2.2.1. Граф И/ИЛИ и поиск данных
Рис. 3.4. Граф И/ИЛИ, используемый для представления процесса вывода
Как было показано, правила состоят из условной и заключительной частей, причем в классическом случае в условной части правила проверяются данные из рабочей памяти (например, проверяется наличие/отсутствие данных либо выполнение условия описания данных с помощью предикатов); она может состоять из одного условия или нескольких условий, соединенных связкой И. Заключительная часть показывает данные, которыми следует дополнить рабочую память при выполнении условной части. На практике при использовании систем продукций в соответствии с необходимостью расширяют эти правила (например, используют связь ИЛИ в условной части, вводят условную часть с вычислениями на основании содержимого рабочей памяти и другими операциями либо вводят заключительную часть, указывающую на заключение без дополнения содержимого рабочей памяти и т. п.), поэтому рассмотренные до сих пор правила можно считать классическими. Подобные правила представляют собой отношение вывода, установленное между содержимым рабочей памяти, ссылка на которое осуществляется из условной части, и содержимым, указываемым. в заключительной части. Визуально такое отношение можно представить в виде графа с древовидной структурой, как показано на рис. 3.2. Добавим, что если существует множество правил, из которых выводится одно и то же заключение, то выполнив операцию ИЛИ над всеми заключениями, получаемыми с помощью этих правил (поскольку даже при выполнении хотя бы одного из них можно получить данное заключение), можно показать отношение между результатом отдельного вывода и данными, на основании которых делается вывод (рис. 3.3). Следовательно, если в такой форме представить отношение между всеми правилами, используемыми в системе продукций, и содержимым памяти, то всю систему продукций можно представить в виде одного графа И/ИЛИ. В самом нижнем узле этого графа будут располагаться основные системные данные, а в самом верхнем узле — заключения, выводимые системой. В итоге вывод, получаемый с помощью системы продукций, можно представить как совокупность серии правил, поддерживающих отдельное заключение, и данных, на основании которых делается вывод. Пример такого графа показан на рис. 3.4. . С помощью такого графа обратный вывод можно представить как проблему поиска пути на данном графе. Другими словами, для подтверждения одной цели из всех связей ИЛИ, определенных по отношению к узлам графа, соответствующим этой цели, выбирается одна и делается попытка подтвердить все узлы, являющиеся предусловиями этой цели. В случае неудачи выбирается следующая связка ИЛИ и повторяется аналогичная процедура. Если обнаружится, что хотя бы одна из связок ИЛИ позволяет вывести последнюю цель, то доказательство (подтверждение) этой цели считается успешным, в противном случае - неуспешным. В данном случае выбор одной из связок ИЛИ есть не что иное, как выбор одного из правил, т.е. снова мы возвращаемся к проблеме разрешения конфликтов. Кроме того, определение последовательности оценки связок И, раскрывающих связки ИЛИ, соответствует последовательности оценки условных частей правил. В играх (например, в шахматах или шашках) проблема поиска на графе, показывающего возможности разворачивания ситуации, является существенной проблемой, поэтому применение эффективных способов поиска — это ключ к успеху. С точки зрения эффективности вывода в системах продукций важной проблемой является способ организации поиска на графе (т. е. разрешение конфликтов и определение последовательности оценки условных частей). В то же время ширина графа И/ИЛИ системы продукций заранее регламентируется числом этапов вывода (от исходных данных до получения заключения) и числом правил„ на основании которых выводится одно и то же заключение, поэтому считается, что случаев, когда невозможно вывести все заключения, сравнительно мало. Это обстоятельство можно назвать преимущественной отличительной особенностью с точки зрения возможности вывода заключения, несмотря на использование машины логического вывода по сравнительно простому алгоритму. Однако, когда ставится цель построения системы, имеющей практическое значение, особую важность приобретает эффективность вывода. Кроме того, когда методом логического вывода регламентируется суммарный объем запрашиваемых данных и последовательность запроса, то число запросов минимизируется. Для того, чтобы запросы выполнялись в естественной последовательности, обычно используют различные методы управления выводом, и это управление определяется последовательностью поиска на графе. Отметим, что часто используется способ приоритетного поиска, т. е. на основе правила с жестким условием. Алгоритмы поиска на графе (например, а — ß-алгоритмы), характерные для игр и т. п., используются сравнительно редко. Кроме того, в системах, имеющих практическое значение, проблема разрешения конфликтов без поиска на графе зачастую зависит от свойств предметной области, поэтому в таких случаях довольно часто используют эвристические методы.
Пример. Имеется фрагмент базы знаний из двух правил: П1: Если "отдых - летом" и "человек - активный", то "ехать в горы", П2: Если "любит солнце", то "отдых летом", Предположим, в систему поступили данные - "человек активный" и "любит "солнце" Прямой вывод - исходя из данных, получить ответ. 1-й проход. Шаг 1. Пробуем П1, не работает (не хватает данных "отдых - летом"). Шаг 2. Пробуем П2, работает, в базу поступает факт "отдых - летом". 2-й проход. Шаг 3. Пробуем П1, работает, активируется цель "ехать в горы", которая и выступает как совет, который дает ЭС. Обратный вывод - подтвердить выбранную цель при помощи имеющихся правил и данных. 1-й проход. Шаг 1. Цель - "ехать в горы": пробуем П1 - данных, "отдых - летом" нет, они становятся новой целью, и ищется правило, где она в правой части. Шаг 2. Цель "отдых - летом": правило П2 подтверждает цель и активирует ее. 2-й проход. Шаг 3. Пробуем П1, подтверждается искомая цель. Продукционная модель чаще всего применяется в промышленных экспертных системах. Она привлекает разработчиков своей наглядностью, высокой модульностью, легкостью внесения дополнений и изменений и простотой механизма логического вывода. Достоинства продукционной модели данных: простая и ясная нотация. Недостатки: при большом количестве правил вывод идет очень долго.
|