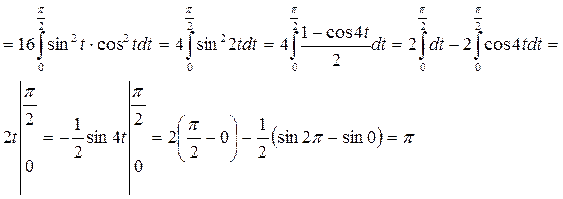Замена переменной в определенном интеграле
Теорема 5. Пусть функция f (x) непрерывна на отрезке [ a;b ] и пусть функция x = j (t) имеет непрерывную производную j '(t) на отрезке [ a; b ], область значений этой функции – отрезок [ a;b ], то есть a £ j (t) £ b для x t Î [ a; b ], причем j (a) = a, j (b) = b. Тогда справедливо равенство:
Доказательство. Так как f (x)непрерывна на [ a;b ], то существует определенный интеграл
где F(x) – одна из первообразных f (x) на [ a;b ]. Известно, что F(x) дифференцируема в любой точке [ a;b ], причем F'(x) = f (x) для любого x Î [ a;b ]. Так как функция x = j (t) непрерывна на [ a; b ] и множество ее значений совпадает с отрезком [ a;b ], то сложные функции f (j (t)) и F(j (t)) непрерывны в любой точке t Î [ a; b ]. Так как j ' (t) непрерывна на [ a; b ], то функция f (j (t)) × j ' (t) тоже непрерывна на [ a; b ], а значит существует интеграл:
Покажем, что функция F(j (t)) является первообразной для
(так как j (b) = b и j (a) = a). (2) Сравнивая результаты (1) и (2) приходим к равенству:
Пример 3.
Ответ: Пример 4.
Ответ: Интегрирование по частям в определенном интеграле Теорема 6. Пусть функции u (x) и V (x) имеют непрерывные производные на [ a; b ]. Тогда справедливо равенство:
|

 .
. и справедлива формула Ньютона-Лейбница:
и справедлива формула Ньютона-Лейбница: (1)
(1) .
. . Действительно, (F(j (t)))' t = F'(x)× j '(t) = f (x)× j' (t) = f (j (t))× j' (t) для любого t Î [ a; b ]. Поэтому можно к этому интегралу применить формулу Ньютона-Лейбница:
. Действительно, (F(j (t)))' t = F'(x)× j '(t) = f (x)× j' (t) = f (j (t))× j' (t) для любого t Î [ a; b ]. Поэтому можно к этому интегралу применить формулу Ньютона-Лейбница: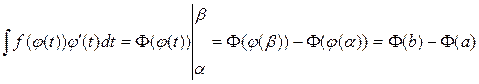
 .
.