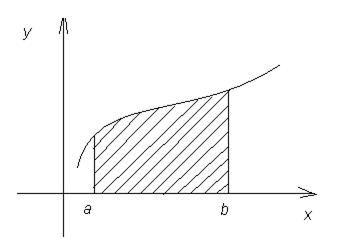
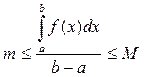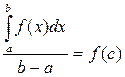Геометрический смысл определенного интеграла
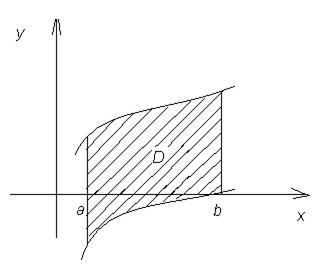
2) Если область ограничена двумя кривыми y = f (x) и y = g (x), причем при xÎ [ a;b ] f (x) ³ g (x), то площадь области ограниченным кривыми y = f (x); y = g (x) и прямыми x = a, x = b вычисляется по формуле:
Свойства определенного интеграла. 1) 2) 3) 4) 5) Если функция f (x) интегрируема на отрезках [ a;c ] и [ c;b ], то она интегрируема и на [ a;b ], причем верно равенство:
При любом расположении точек a, b и c на оси Ox. 6) Если f (x) ³ 0 при xÎ; [ a;b ], то
7) Если на [ a;b ] f (x) ³ g (x), то
8) Теорема 2 (о среднем значении определенного интеграла). Если функция f (x) непрерывна на [ a;b ], то на этом отрезке найдется хотя бы одна точка c, в которой выполняется равенство:
Доказательство:Так как f (x) на [ a;b ] непрерывна, то она достигает на этом отрезке своих наименьшего “ m ” и наибольшего “ M ” значений. Тогда m £ f (x) £ M для любого x Î [ a;b ]. По свойству 7 определенного интеграла можно записать неравенство:
Так как m и M – постоянные числа, то
Вычислим по определению определенного интеграла
Тогда неравенство (*) можно переписать:
Разделим все части полученного неравенства на (b - a) > 0 (длина отрезка интегрирования):
Так как f (x) непрерывна на [ a;b ], тона принимает все значения, заключенные между наименьшим “ m ” и наибольшим “ M ” значениями. Значит найдется на [ a;b ] хотя бы одна точка c, в которой выполняется равенство:
Вычисление определенного интеграла
|

 .
.

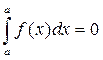
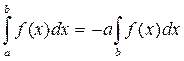
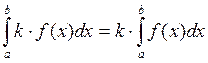

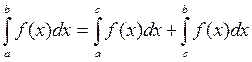

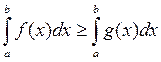

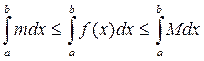
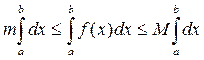 (*)
(*)