Интегралы от разрывных функций
1) Пусть функция y = f (x) определена и непрерывна на промежутке [ a; b ], а в точке x = b либо не определена, либо имеет разрыв. Такую точку x = b будем называть особой точкой функции f (x). Определение 2. Если существует конечный предел
Если конечный предел не существует или он бесконечный, то говорят, что несобственный интеграл 2) Пусть функция y = f (x) определена и непрерывна на промежутке [ a; b ], а в точке x = a либо не определена, либо имеет разрыв. Такую точку x = a называют особой точкой функции f (x). Определение 3. Если существует конечный предел
При этом говорят, что несобственный интеграл
Если конечный предел не существует или бесконечен, то говорят, что несобственный интеграл Замечание. Если функция f (x) имеет разрыв в некоторой точке x = c внутри отрезка [ a; b ], то по определению полагают:
при условии, что оба предела в правой части существуют, и e и d не зависят друг от друга. Этот интеграл также называют несобственным интегралом второго рода от функции f (x) на отрезке [ a; b ] и обозначается символом:
Сходимость или расходимость такого интеграла зависит от существования или не существования конечного предела.
Пример 2. Исследовать на сходимость:
Так получили конечное число, то Ответ: Пример 3. Исследовать на сходимость:
Так как получили конечное число, то Ответ: Пример 4. Исследовать на сходимость:
Так получили бесконечность, то Ответ: расходится
|

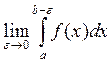 , то он называется несобственным интегралом второго рода от функции f (x) на отрезке [ a; b ] и обозначается символом
, то он называется несобственным интегралом второго рода от функции f (x) на отрезке [ a; b ] и обозначается символом 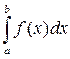 . При этом говорят, что несобственный интеграл
. При этом говорят, что несобственный интеграл 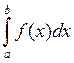 сходится и пишут равенство:
сходится и пишут равенство: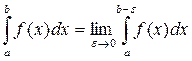 .
.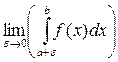 , то он называется несобственным интегралом второго рода от функции f (x) на отрезке [ a; b ] и обозначается символом:
, то он называется несобственным интегралом второго рода от функции f (x) на отрезке [ a; b ] и обозначается символом: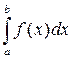 .
.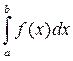 сходится и пишут равенство:
сходится и пишут равенство: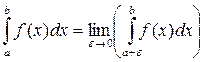 .
.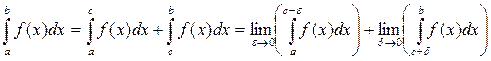
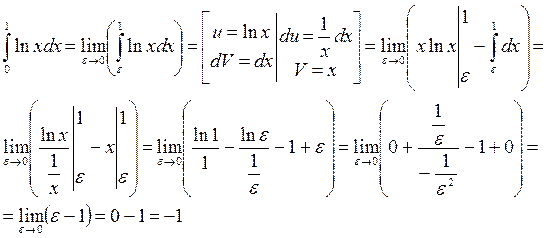
 сходится и равен «-1».
сходится и равен «-1».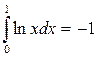
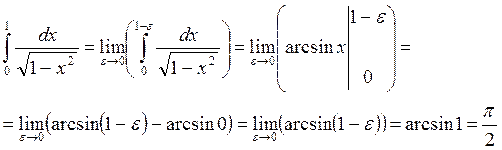
 сходится и равен
сходится и равен 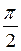 .
.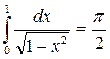
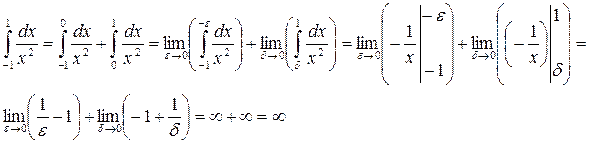
 расходится.
расходится.


